How to Determine Forecastability of Demand?

Data Science, eCommerce, Marketing, Statistics

How to Determine Forecastability of Demand?

In demand forecasting, there are a lot of cases where data scientists struggle to reach a good forecast error. On these occasions, they find it difficult to provide clear explanation to why some threshold of error is un-attainable no matter what technique is used. Forecast error of a product / event highly depends on its forecastability. If some event is unforecastable, it doesn’t even make sense to create a forecast model for it. We can rely on two parameters in order to determine whether the event is forecastable or not:

ADI (Average Demand Interval) – Represents the measure of intermittency.

ADI = Total Number of Period / Number of non-zero demand occasions

CV² (Squared Coefficient of Variation) – Represents the measure of variation excluding zero demand events.

CV² = Standard Deviation of Population /  Average of Population

Based on these two parameters, we can classify the demand profile into one of these 4 different classes:

Smooth Demand

Erratic Demand

Intermitted Demand

Lumpy Demand

Smooth Demand

ADI < 1.32 & CV² < 0.49 is classified as Smooth Demand because the demand is very regular in magnitude and occurrence. This class is very easy to forecast and low forecast error is attainable.

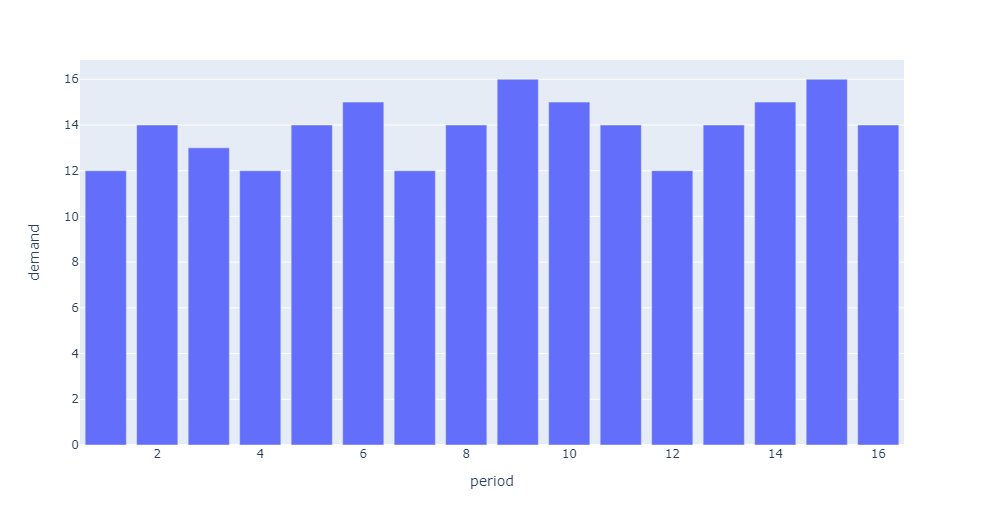
Erratic Demand

ADI < 1.32 & CV² >= 0.49 is classified as Erratic Demand because the demand is irregular in magnitude even-though it is in regular occurrence. Low forecast error will be hard to attain.

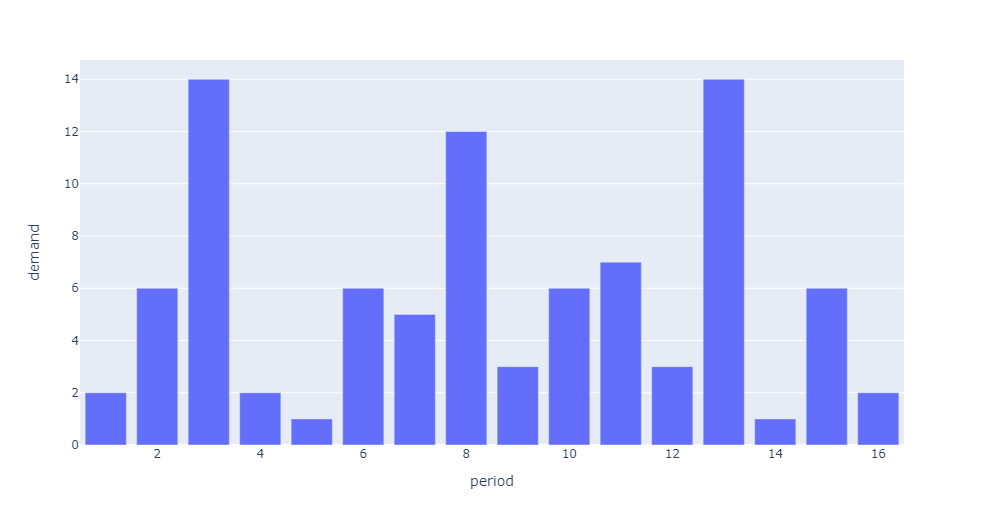
Intermittent Demand

ADI >= 1.32 & CV² < 0.49 is classified as Intermittent Demand because the demand is very regular in magnitude but it is very irregular in occurrence. Low forecast error will be hard to attain.

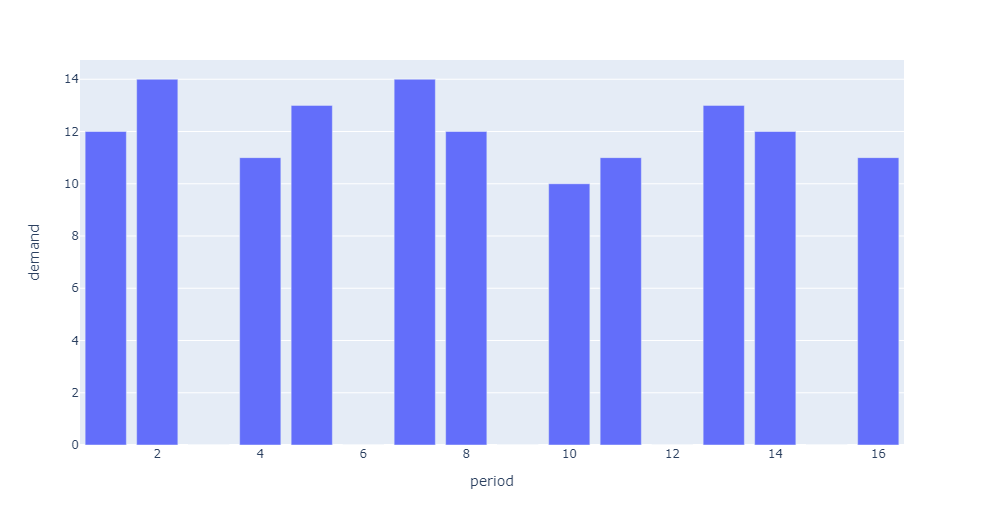
Lumpy Demand

ADI >= 1.32 & CV² >= 0.49 is classified as Lumpy demand because the demand is very irregular in magnitude and occurrence. It is improbable to create a forecast model that can have some predictability. Lumpy demand is unforecastable.

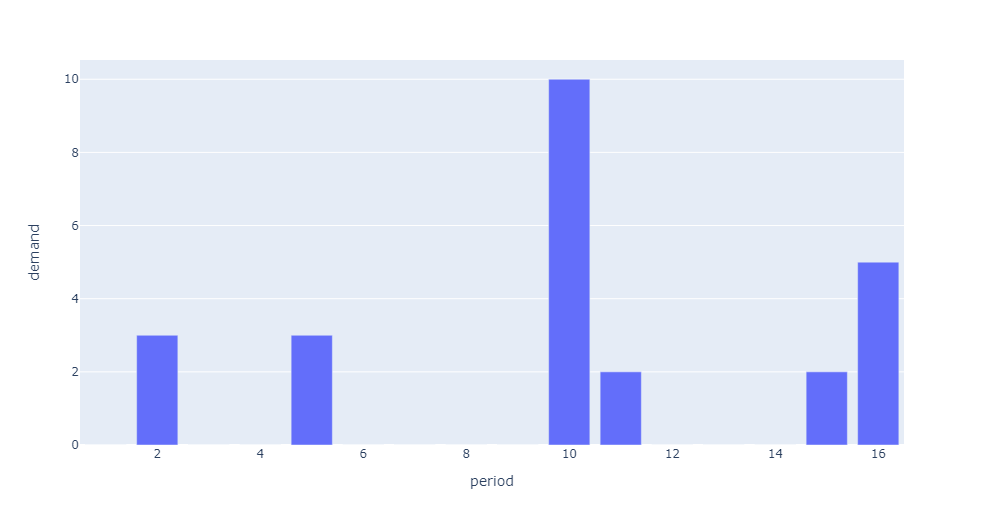
Determining the classification of historical demand makes it easy to plan out the research and development of a demand forecast model. This includes but no restricted to: