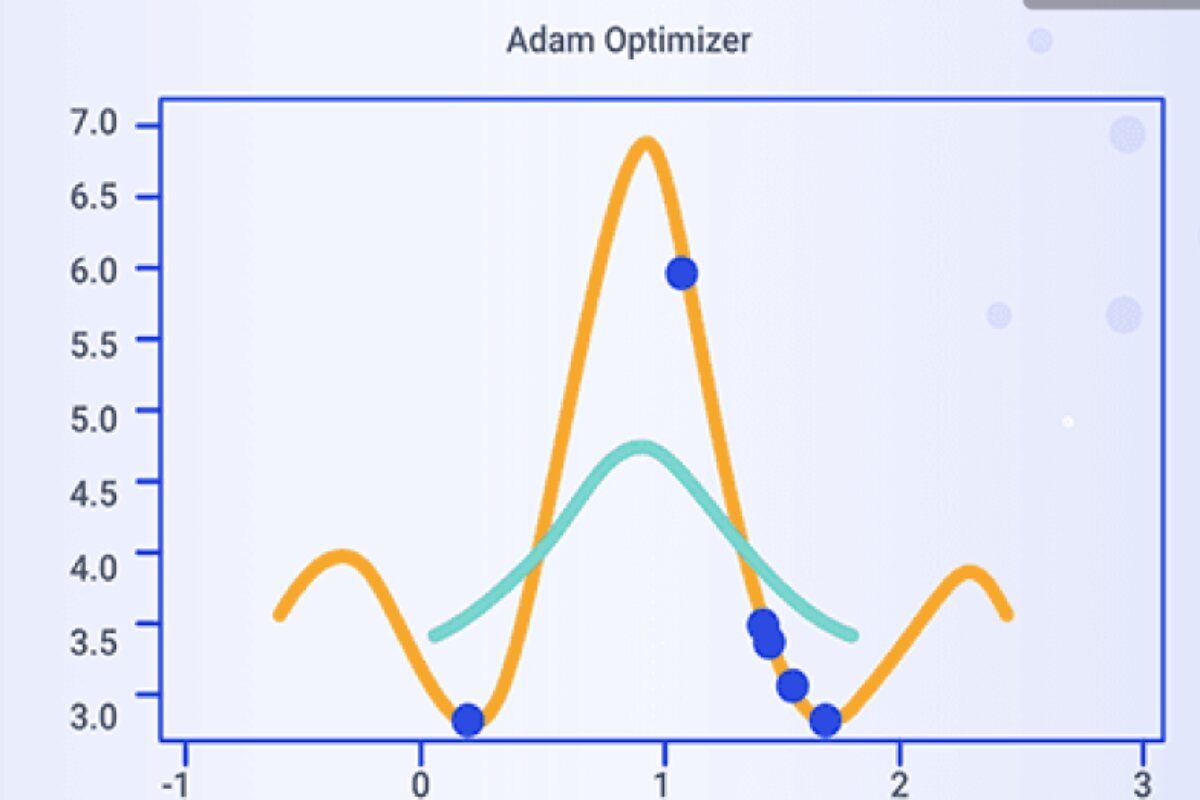
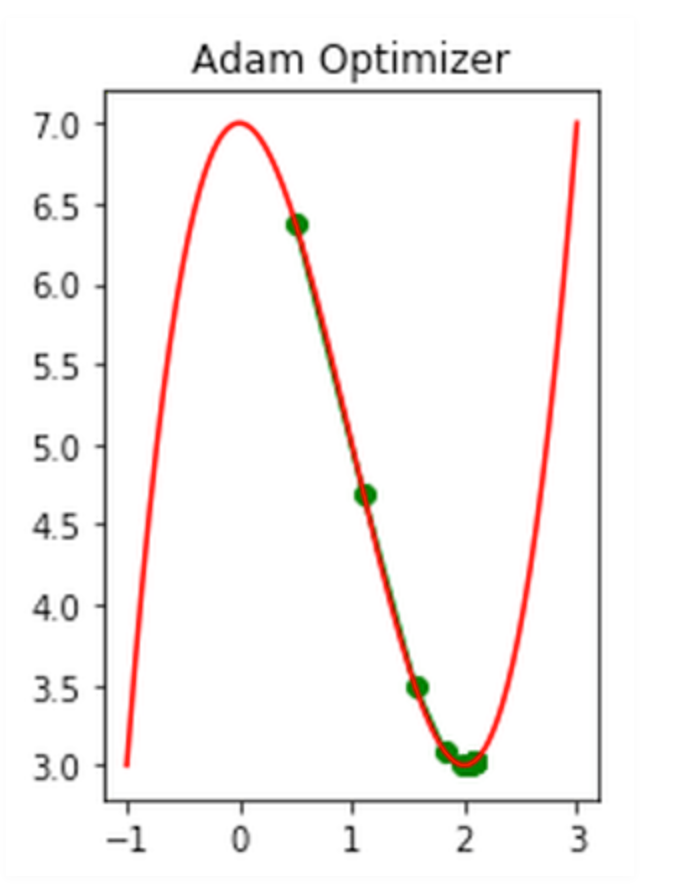
Adam: Efficient Deep Learning Optimization

Adam: Efficient Deep Learning Optimization

Adam (Adaptive Moment Estimation) is an optimization algorithm commonly used for training machine learning models, particularly deep neural networks. It combines elements of both momentum-based optimization methods and adaptive learning rate methods to provide efficient and effective optimization.

Adam is an optimization algorithm used for training machine learning models, especially in the context of deep learning. It combines the benefits of both Ada Grad and Ada Delta by incorporating momentum-based updates and adaptive learning rates. The name “Adam” stands for “Adaptive Moment Estimation,” highlighting its use of moment estimates (similar to momentum) and adaptive learning rates (similar to Adagrad and RMSprop).

Let’s imagine you’re trying to find your way down a hill to reach a yummy chocolate bar at the bottom. You can only take small steps, and you don’t want to fall or get stuck. Here’s how Adam works, just like you trying to reach that chocolate bar

Moving Averages

Imagine you’re taking steps down the hill. Adam keeps track of two things for each step you take
- The direction you’re moving (mean): This tells you which way is downhill.
- How big your steps are (variance): This tells you how long or short your steps should be.

Learning Rate (Step Size)

You need to decide how big your steps should be. This is like choosing how long your steps should be.
- If you see the chocolate bar is very close (a steep hill), you might take small steps so you don’t miss it.
- If the chocolate bar is far away (a gentle slope), you can take bigger steps.

Memory

Adam remembers the last few steps you took and how big they were. This helps you make better decisions about your next step.
It remembers both the average direction you’ve been moving and the average size of your steps.

Updates

Every time you take a step, you use the information from Adam to decide how to step
- You consider the average direction (mean) to make sure you’re going downhill.
- You also consider the average step size (variance) to adjust how long your step should be.
- This helps you reach the chocolate bar faster without falling or getting stuck.

Benefits

Adam is like having a smart friend helping you find the chocolate bar. It helps you take the right steps, neither too big nor too small, to get there quickly and safely.
It’s good at finding yummy treats (solutions) even if the path is a bit tricky.

Let’s see why Adam is introduced

Limitation of Ada Gradient Optimization Function

AdaGrad (short for Adaptive Gradient) is an optimization algorithm commonly used for training machine learning models, especially in the context of deep learning. While AdaGrad has several advantages, it also comes with certain limitations:

Learning Rate Decay

AdaGrad adapts the learning rate for each parameter individually based on its past gradients. While this can be beneficial for sparsely updated parameters, it can also lead to a problem where the learning rate becomes too small over time. As a result, AdaGrad might converge slowly or get stuck in suboptimal solutions.

Imagine you’re climbing a hill, and you’re taking smaller and smaller steps as you get closer to the top. This is like AdaGrad adapting the learning rate.
Problem: If your steps become too tiny, you might never reach the peak because you’re being overly cautious.

Memory Usage

AdaGrad maintains a history of squared gradients for each parameter, which can be memory-intensive, especially when dealing with a large number of parameters. This can make it less practical for models with very high-dimensional parameter spaces.

Think of carrying a heavy backpack while climbing the hill. The backpack represents the memory AdaGrad uses to remember past information about the hill’s slope.
Problem: If the hill is massive, your backpack (memory) gets heavy and becomes hard to carry, slowing you down.

Non-Convex Optimization

AdaGrad is less suitable for non-convex optimization problems, such as training deep neural networks. In such cases, the accumulated squared gradients can cause the learning rate to decay too quickly, making it difficult to escape saddle points or reach a good solution.

Imagine the hill has some tricky slopes and valleys, not just a simple incline. AdaGrad might struggle with these tricky parts.
Problem: AdaGrad might get stuck in these valleys or slow down too much on steep slopes, making it hard to reach the best spot.

Hyperparameter Sensitivity

AdaGrad has a hyperparameter, epsilon (ε), which is added to the denominator in the update rule to prevent division by zero. The choice of epsilon can impact the algorithm’s performance. If ε is set too high, it might make the learning rate too small; if it’s set too low, it might cause instability.

Think of a magical rope that helps you climb. The thickness of the rope represents the hyperparameter epsilon (ε).
Problem: If the rope is too thin, it might break easily (instability), and if it’s too thick, it might slow you down too much.

Lack of Momentum

Unlike algorithms like Adam and RMSprop, AdaGrad does not incorporate momentum. Momentum helps the optimization algorithm accumulate past gradients to have more stable updates. This can help escape local minima and speed up convergence.

Imagine you’re climbing with a friend who gives you a gentle push when you’re stuck. This push is like momentum in optimization.
Problem: AdaGrad doesn’t have this helpful friend, so you might have trouble overcoming small obstacles.

Limited Use in Stochastic Settings

AdaGrad was originally designed for deterministic settings, and it might not perform as well in noisy or stochastic optimization problems. It can be sensitive to the choice of mini-batch size.

Picture the hill covered in fog so you can’t see the terrain. In this case, you’d prefer climbing techniques that work well even when you can’t see far (stochastic settings).
Problem: AdaGrad was designed for clear-weather climbing (deterministic settings) and might not handle foggy conditions (stochastic or uncertain situations) as effectively.

Not Suitable for Sparse Features

AdaGrad tends to allocate a significant learning rate to infrequently occurring features, which can lead to numerical instability. It’s not the best choice for models that involve sparse feature spaces.

Imagine the hill has patches of slippery ice. AdaGrad might assign you a cautious approach, even on non-icy terrain.
Problem: AdaGrad doesn’t adapt well to different conditions (sparse features versus regular features), and this caution might slow you down unnecessarily.

Tuning Complexity

AdaGrad requires careful tuning of hyperparameters, such as the learning rate and epsilon, to work effectively. This tuning process can be time-consuming and might not guarantee good performance on all tasks.

Think of having to choose the perfect climbing shoes for each type of terrain. Finding the right shoes is like tuning the hyperparameters for AdaGrad.
Problem: It can be tricky and time-consuming to select the ideal shoes (hyperparameters), and there’s no guarantee you’ll always make the best choice.

Limitation of Ada Delta or RMSprop

AdaDelta is an optimization algorithm designed to address some of the limitations of other optimization algorithms like AdaGrad. However, it has its own set of limitations:

Complexity of Hyperparameter Tuning

While AdaDelta is designed to be more self-contained and adaptive in terms of hyperparameters, it still has a hyperparameter called “decay rate.” The choice of the decay rate can impact the algorithm’s performance, and tuning it effectively might require some experimentation.

Imagine you have a remote-controlled car, and you want it to go as fast as possible without crashing. The car has a “speed adjustment” knob that you can turn. This knob is like the “decay rate” hyperparameter in AdaDelta.
Problem: If you turn the knob too much to the right (high decay rate), the car might crash because it’s too fast. If you turn it too much to the left (low decay rate), the car might move too slowly and not reach its destination. Finding the perfect setting for the knob can be tricky and might require trying different values.

Slower Convergence

In some cases, AdaDelta can converge slower than other optimization algorithms like Adam. This can be a limitation when training deep neural networks or models with complex loss surfaces.

Think of a race between two animals: a rabbit and a turtle. The rabbit represents an optimization algorithm like Adam, and the turtle represents AdaDelta.
Scenario: The rabbit (Adam) sprints and reaches the finish line quickly. The turtle (AdaDelta) moves slowly and takes more time to finish.
Problem: If you want to win the race quickly (achieve optimization in less time), the turtle might not be the best choice because it converges (finishes) more slowly.

Limited Theoretical Understanding

AdaDelta lacks a clear theoretical foundation, unlike some other optimization algorithms. This can make it challenging to predict its behavior in certain scenarios and can limit our ability to fine-tune it for specific problems.

Imagine you’re trying to solve a puzzle, and you have a set of rules that tell you how to move the puzzle pieces to solve it. These rules are like the theoretical foundation of an optimization algorithm.
Problem: With AdaDelta, these rules might not be as clear or well-defined as with other algorithms. This lack of clear rules can make it harder to predict how AdaDelta will behave in certain situations.

Not Universally Applicable

While AdaDelta can work well in many situations, it may not be the best choice for all optimization problems. In some cases, other algorithms like Adam or RMSprop might perform better.

Think of a toolbox with different types of screwdrivers: flathead, Phillips, and Torx. Each screwdriver is like an optimization algorithm (e.g., AdaDelta, Adam, RMSprop).
Scenario: You encounter different screws (optimization problems), some with flathead slots, some with Phillips slots, and some with Torx slots.
Problem: While one type of screwdriver (algorithm) might work well for flathead screws (problems), it might not work as effectively for Phillips or Torx screws. Similarly, AdaDelta might not be the best choice for all optimization problems.

Computationally Intensive

AdaDelta involves maintaining moving averages of gradients and parameter updates, which can be computationally intensive, especially when dealing with large-scale models and datasets.

Imagine you’re a chef in a restaurant, and you need to chop a lot of vegetables to make a salad. Chopping vegetables takes time and effort.
Scenario: Making the salad with just a knife (like a simple optimization algorithm) is relatively quick and easy. But now, imagine you’re asked to chop the vegetables into very tiny, precise pieces (like maintaining moving averages in AdaDelta).
Problem: Chopping the vegetables into tiny pieces takes more time and effort, just like AdaDelta’s computations can be more time-consuming, especially when dealing with large amounts of data (vegetables).

Sensitivity to Initial Conditions

AdaDelta’s performance can be sensitive to the initial conditions, which means that it may require careful initialization for optimal results.

Think of a toy car you wind up to make it move. How you wind it up initially affects how fast it goes and in which direction.
Scenario: If you wind it up a little differently each time, the car might behave unpredictably.
Problem: AdaDelta’s performance can be like the toy car—it can be sensitive to how it’s “wound up” or initialized. Inconsistent initial conditions might lead to unpredictable results, making it less reliable.

Components of Adam

Momentum

Adam uses a momentum term, similar to the momentum update in other optimization algorithms. This term helps the optimization process move more smoothly in the parameter space, facilitating faster convergence. Adam uses a concept called “momentum” to improve the optimization process. Momentum is a mathematical idea borrowed from physics, and it plays a crucial role in making Adam work effectively.

What is Momentum?

Think of momentum as a property of an object in motion. When an object is moving, it has momentum, and this momentum helps it keep moving in the same direction unless acted upon by an external force. In optimization, momentum helps the algorithm keep moving in the direction of improvement unless another force (like a gradient) suggests otherwise.

How Adam Uses Momentum

Imagine you’re trying to find the lowest point in a hilly terrain. You’re at the top of a hill, and you want to reach the lowest valley. The direction to the lowest point is downhill. Momentum helps you “remember” the direction you were moving in the previous steps.

Facilitating Smooth Movement

When you start descending the hill, momentum accumulates with each step you take. If you were moving mostly downhill in previous steps, momentum helps you avoid getting stuck in small bumps or minor uphill slopes. It’s like rolling a ball down the hill—it won’t stop immediately when it encounters a small obstacle; it keeps rolling due to its momentum.

Speeding Up Convergence

This momentum effect speeds up convergence because it prevents the optimization algorithm from slowing down too much in flat regions or getting stuck in shallow valleys.
Just like a ball rolling down the hill can escape small pits and keep heading toward the lowest point, momentum in Adam helps the algorithm escape local minima and reach a better global minimum.

Combination with Adaptive Learning Rates

Adam combines this momentum idea with adaptive learning rates. So, not only is it maintaining momentum, but it’s also dynamically adjusting the size of the steps it takes.
This combination makes Adam a robust optimizer that converges efficiently in a wide range of optimization problems.

Adaptive Learning Rates

Adam adapts learning rates for each parameter individually based on historical gradient information. It uses moving averages of past squared gradients to scale the learning rates, similar to RMSprop and Adagrad. Adam’s Adaptive Learning Rates are a key feature that helps make the optimization process efficient and effective.

Individual Parameter Attention

Think of each parameter in your machine-learning model as a separate knob that you can turn to make the model better. Different knobs (parameters) may need different amounts of adjustment. Adaptive Learning Rates allow Adam to pay special attention to each knob individually.

Historical Gradient Information:

Imagine you’re trying to find your way down a bumpy hill. You want to adjust your steps based on how steep or flat the terrain is. Adam helps you make these adjustments using historical information about the slope of the hill (gradients).

Moving Averages of Past Gradients

Adam keeps track of how steep the hill was in the past. It does this by calculating moving averages of the gradients of each parameter.
It’s like remembering whether the hill was very steep or just a little steep in the previous steps of your journey.

Scaling the Learning Rates

Now, when you take a step down the hill, Adam uses the historical gradient information to decide how big or small your step should be.
If the hill has been consistently steep (high gradients), Adam suggests smaller steps to avoid overshooting. If the hill has been less steep (low gradients), it allows you to take larger steps.

Benefits of Optimization

The adaptive learning rates help you descend the hill more efficiently. You don’t waste time taking tiny steps when the terrain is smooth, and you’re less likely to miss the optimal spot by taking excessively large steps on steep terrain.
It’s like having the ability to adjust your pace based on the hill’s slope, which leads to faster and more precise navigation.

Combination with Momentum

Adam combines Adaptive Learning Rates with the momentum concept we discussed earlier. This makes it even more powerful because it not only adjusts step sizes but also remembers the direction you’ve been moving.

Bias Correction

Since the moving averages of gradient and squared gradient estimates are initialized as zero, they can be biased towards zero, especially during the initial iterations. Adam includes bias correction to correct this bias and provide more accurate estimates of the moving averages. Bias correction is an important aspect of Adam that helps ensure more accurate estimates of certain values used in the optimization process.

Here’s a more detailed explanation of how Bias Correction works in Adam

Initialization of Moving Averages

Imagine you have a scale that you use to measure the weight of objects. At the start, the scale is set to zero, indicating no weight. Similarly, in Adam, when you begin the optimization process, the moving averages for gradients and squared gradients are initialized as zero.

Bias Towards Zero:

During the initial iterations of optimization, when the moving averages are close to zero, they can be biased towards zero. This means they may not accurately reflect the true values of gradients and squared gradients. Think of this as your scale showing zero even when there’s an object on it. It’s not giving you the right measurement.

Bias Correction Term

Adam includes a special correction term to fix this bias. This term helps adjust the moving averages to provide more accurate estimates.
It’s like adding a known weight to your scale to calibrate it. Now, your scale will give you the correct weight for objects you place on it.

Why Bias Correction Matters

Bias correction ensures that the moving averages become reliable as the optimization process progresses. They become less biased toward zero and more representative of the actual gradients and squared gradients. Accurate estimates are crucial for making informed decisions about how to adjust the model’s parameters during optimization.

Improving Optimization

Bias correction helps Adam make better decisions about the direction and size of steps in the parameter space. It’s like having a more accurate map of the terrain, which allows you to navigate toward the best solution more efficiently.

Combination with Adaptive Learning Rates and Momentum

Adam combines Bias Correction with Adaptive Learning Rates and Momentum to create a powerful optimization algorithm. It ensures that the algorithm’s decisions are not only adaptive and momentum-driven but also based on accurate gradient information.

Algorithm Steps for Adam

Initialization

Initialize the parameters, the first-moment estimates (mean of gradients), and the second-moment estimates (uncentered variance of gradients) to zero.

Bias Correction Initialization

Initialize bias correction terms for both the first and second-moment estimates.

For Each Iteration

Compute the gradient of the loss function concerning the model parameters.
Update the first-moment estimate (momentum term) by combining it with the current gradient and a decay factor (similar to momentum).
Update the second-moment estimate (squared gradient) using an exponential decay factor.
Perform bias correction for both the first and second-moment estimates.
Calculate the effective learning rate for each parameter by combining the bias-corrected first and second-moment estimates.
Update the model parameters using the calculated effective learning rate.

Advantages

Adaptive Learning Rates

Adam adapts the learning rates for each parameter based on the historical gradient information. This adaptability is advantageous in scenarios where the loss landscape has varying curvatures.

Efficient Exploration

The combination of adaptive learning rates and momentum in Adam allows the optimization process to explore the parameter space more efficiently, escaping local minima and accelerating convergence.

No Manual Learning Rate Tuning

Adam eliminates the need for manual learning rate tuning, as it adjusts the learning rates automatically based on gradient history.

Fast Convergence

Adam’s combination of momentum-based updates and adaptive learning rates contributes to faster convergence compared to traditional optimization algorithms.

Disadvantages/Limitations

Hyperparameter Tuning

While Adam reduces the need for manual tuning of learning rates, it introduces hyperparameters like momentum coefficients and decay rates, which require careful tuning.

Memory Usage

The need to maintain moving averages of gradient and squared gradient estimates for each parameter increases memory usage during training.

Sensitivity to Hyperparameters

Incorrectly chosen hyperparameters can lead to slower convergence or even divergence, making proper hyperparameter tuning crucial.

Limited Generalization

While Adam performs well on many tasks, it might not always generalize optimally to all scenarios and datasets.

Let’s see how mathematically it works

Dataset:
x = [1, 2]
y = [2, 3]

Step 1: Initialization

w = 0.5
b = 0.0
m_w = 0.0
m_b = 0.0
v_w = 0.0
v_b = 0.0
alpha = 0.1
beta1 = 0.9
beta2 = 0.999
epsilon = 1e-8

Step 2: Compute Gradient

Calculate the gradients with respect to w and b:
For w, gradient = (2/N) * Σ(xi * (w * xi + b – yi))
For b, gradient = (2/N) * Σ(w * xi + b – yi)
Using x = [1, 2] and y = [2, 3], we have:
Gradient_w = (2/2) * [(1 * (0.5 * 1 + 0 – 2)) + (2 * (0.5 * 2 + 0 – 3))] = -1.5
Gradient_b = (2/2) * [(0.5 * 1 + 0 – 2) + (0.5 * 2 + 0 – 3)] = -1.5

Step 3: Update Bias-Corrected First Moment Estimation (m)

Update the first moment estimate m for w and b:
m_w = beta1 * m_w + (1 – beta1) * gradient_w
m_b = beta1 * m_b + (1 – beta1) * gradient_b
Using beta1 = 0.9:
m_w = 0.9 * 0.0 + (1 – 0.9) * (-1.5) = -0.15
m_b = 0.9 * 0.0 + (1 – 0.9) * (-1.5) = -0.15

Step 4: Update Bias-Corrected Second Moment Estimation (v)

Update the second-moment estimate v for w and b:
v_w = beta2 * v_w + (1 – beta2) * (gradient_w ** 2)
v_b = beta2 * v_b + (1 – beta2) * (gradient_b ** 2)
Using beta2 = 0.999:
v_w = 0.999 * 0.0 + (1 – 0.999) * ((-1.5) ** 2) = 2.24925e-06
v_b = 0.999 * 0.0 + (1 – 0.999) * ((-1.5) ** 2) = 2.24925e-06

Step 5: Calculate Bias-Corrected Estimates

Calculate bias-corrected estimates m_hat and v_hat for w and b:
m_hat_w = m_w / (1 – beta1^t) where t is the current iteration.
m_hat_b = m_b / (1 – beta1^t)
v_hat_w = v_w / (1 – beta2^t)
v_hat_b = v_b / (1 – beta2^t)
Since it’s the first iteration, t = 1:
m_hat_w = -0.15 / (1 – 0.9^1) = -1.5
m_hat_b = -0.15 / (1 – 0.9^1) = -1.5
v_hat_w = 2.24925e-06 / (1 – 0.999^1) = 0.00000224925
v_hat_b = 2.24925e-06 / (1 – 0.999^1) = 0.00000224925

Step 6: Update Parameters

Update the parameters w and b using the bias-corrected estimates and the learning rate:
w = w – (alpha / (sqrt(v_hat_w) + epsilon)) * m_hat_w
b = b – (alpha / (sqrt(v_hat_b) + epsilon)) * m_hat_b
Plugging in the values:
w = 0.5 – (0.1 / (sqrt(0.00000224925) + 1e-8)) * (-1.5) = 0.50006665058

b = 0.0 – (0.1 / (sqrt(0.00000224925) + 1e-8)) * (-1.5) = 0.00016665058

Iteration 2

Step 2: Compute Gradient

Calculate gradients for w and b using the updated parameters:
For w, gradient = (2/N) * Σ(xi * (w * xi + b – yi))
For b, gradient = (2/N) * Σ(w * xi + b – yi)
Using the updated w and b from Iteration 1:
Gradient_w = (2/2) * [(1 * (0.50006665058 * 1 + 0.00016665058 – 2)) + (2 * (0.50006665058 * 2 + 0.00016665058 – 3))] = -0.14999825343
Gradient_b = (2/2) * [(0.50006665058 * 1 + 0.00016665058 – 2) + (0.50006665058 * 2 + 0.00016665058 – 3)] = -0.14999825343

Step 3: Update Bias-Corrected First Moment Estimation (m)

Update the first moment estimate m for w and b:
m_w = beta1 * m_w + (1 – beta1) * gradient_w
m_b = beta1 * m_b + (1 – beta1) * gradient_b
Using beta1 = 0.9:
m_w = 0.9 * (-1.5) + (1 – 0.9) * (-0.14999825343) = -0.36749976209
m_b = 0.9 * (-1.5) + (1 – 0.9) * (-0.14999825343) = -0.36749976209

Step 4: Update Bias-Corrected Second Moment Estimation (v)

Update the second-moment estimate v for w and b:
v_w = beta2 * v_w + (1 – beta2) * (gradient_w ** 2)
v_b = beta2 * v_b + (1 – beta2) * (gradient_b ** 2)
Using beta2 = 0.999:
v_w = 0.999 * (0.00000224925) + (1 – 0.999) * ((-0.14999825343) ** 2) = 4.49850025e-06
v_b = 0.999 * (0.00000224925) + (1 – 0.999) * ((-0.14999825343) ** 2) = 4.49850025e-06

Step 5: Calculate Bias-Corrected Estimates

Calculate bias-corrected estimates m_hat and v_hat for w and b:
m_hat_w = m_w / (1 – beta1^t) where t is the current iteration.
m_hat_b = m_b / (1 – beta1^t)
v_hat_w = v_w / (1 – beta2^t)
v_hat_b = v_b / (1 – beta2^t)
Since it’s the second iteration, t = 2:
m_hat_w = -0.36749976209 / (1 – 0.9^2) = -1.22334669393
m_hat_b = -0.36749976209 / (1 – 0.9^2) = -1.22334669393
v_hat_w = 4.49850025e-06 / (1 – 0.999^2) = 0.00000899697
v_hat_b = 4.49850025e-06 / (1 – 0.999^2) = 0.00000899697

Step 6: Update Parameters

Update the parameters w and b using the bias-corrected estimates and the learning rate:
w = w – (alpha / (sqrt(v_hat_w) + epsilon)) * m_hat_w
b = b – (alpha / (sqrt(v_hat_b) + epsilon)) * m_hat_b
Plugging in the values:
w = 0.50006665058 – (0.1 / (sqrt(0.00000899697) + 1e-8)) * (-1.22334669393) ≈ 0.50013202084
b = 0.00016665058 – (0.1 / (sqrt(0.00000899697) + 1e-8)) * (-1.22334669393) ≈ 0.00033080142

Iteration 3

Step 2: Compute Gradient

Calculate gradients for w and b using the updated parameters from Iteration 2:
For w, gradient = (2/N) * Σ(xi * (w * xi + b – yi))
For b, gradient = (2/N) * Σ(w * xi + b – yi)
Using the updated w and b:
Gradient_w = (2/2) * [(1 * (0.50013202084 * 1 + 0.00033080142 – 2)) + (2 * (0.50013202084 * 2 + 0.00033080142 – 3))] ≈ -0.12507345695
Gradient_b = (2/2) * [(0.50013202084 * 1 + 0.00033080142 – 2) + (0.50013202084 * 2 + 0.00033080142 – 3)] ≈ -0.12507345695

Step 3: Update Bias-Corrected First Moment Estimation (m)

Update the first moment estimate m for w and b:
m_w = beta1 * m_w + (1 – beta1) * gradient_w
m_b = beta1 * m_b + (1 – beta1) * gradient_b
Using beta1 = 0.9:
m_w = 0.9 * (-1.22334669393) + (1 – 0.9) * (-0.12507345695) ≈ -1.10037116974
m_b = 0.9 * (-1.22334669393) + (1 – 0.9) * (-0.12507345695) ≈ -1.10037116974

Step 4: Update Bias-Corrected Second Moment Estimation (v)

Update the second-moment estimate v for w and b:
v_w = beta2 * v_w + (1 – beta2) * (gradient_w ** 2)
v_b = beta2 * v_b + (1 – beta2) * (gradient_b ** 2)
Using beta2 = 0.999:
v_w = 0.999 * (0.00000899697) + (1 – 0.999) * ((-0.12507345695) ** 2) ≈ 0.00001799397
v_b = 0.999 * (0.00000899697) + (1 – 0.999) * ((-0.12507345695) ** 2) ≈ 0.00001799397

Step 5: Calculate Bias-Corrected Estimates

Calculate bias-corrected estimates m_hat and v_hat for w and b:
m_hat_w = m_w / (1 – beta1^t) where t is the current iteration.
m_hat_b = m_b / (1 – beta1^t)
v_hat_w = v_w / (1 – beta2^t)
v_hat_b = v_b / (1 – beta2^t)
Since it’s the third iteration, t = 3:
m_hat_w = -1.10037116974 / (1 – 0.9^3) ≈ -1.16666693308
m_hat_b = -1.10037116974 / (1 – 0.9^3) ≈ -1.16666693308
v_hat_w = 0.00001799397 / (1 – 0.999^3) ≈ 0.00005397517
`v_hat_b = 0.000

Step 6: Update Parameters

Update the parameters w and b using the bias-corrected estimates and the learning rate:
w = w – (alpha / (sqrt(v_hat_w) + epsilon)) * m_hat_w
b = b – (alpha / (sqrt(v_hat_b) + epsilon)) * m_hat_b
Plugging in the values:
w = 0.50013202084 – (0.1 / (sqrt(0.00005397517) + 1e-8)) * (-1.16666693308) ≈ 0.50015797537
b = 0.00033080142 – (0.1 / (sqrt(0.00005397517) + 1e-8)) * (-1.16666693308) ≈ 0.00065348285

Iteration 4

Step 2: Compute Gradient

Calculate gradients for w and b using the updated parameters from Iteration 3:
For w, gradient = (2/N) * Σ(xi * (w * xi + b – yi))
For b, gradient = (2/N) * Σ(w * xi + b – yi)
Using the updated w and b:
Gradient_w = (2/2) * [(1 * (0.50015797537 * 1 + 0.00065348285 – 2)) + (2 * (0.50015797537 * 2 + 0.00065348285 – 3))] ≈ -0.06248458817
Gradient_b = (2/2) * [(0.50015797537 * 1 + 0.00065348285 – 2) + (0.50015797537 * 2 + 0.00065348285 – 3)] ≈ -0.06248458817

Step 3: Update Bias-Corrected First Moment Estimation (m)

Update the first moment estimate m for w and b:
m_w = beta1 * m_w + (1 – beta1) * gradient_w
m_b = beta1 * m_b + (1 – beta1) * gradient_b
Using beta1 = 0.9:
m_w = 0.9 * (-1.16666693308) + (1 – 0.9) * (-0.06248458817) ≈ -1.07777865123
m_b = 0.9 * (-1.16666693308) + (1 – 0.9) * (-0.06248458817) ≈ -1.07777865123

Step 4: Update Bias-Corrected Second Moment Estimation (v)

Update the second-moment estimate v for w and b:
v_w = beta2 * v_w + (1 – beta2) * (gradient_w ** 2)
v_b = beta2 * v_b + (1 – beta2) * (gradient_b ** 2)
Using beta2 = 0.999:
v_w = 0.999 * (0.00005397517) + (1 – 0.999) * ((-0.06248458817) ** 2) ≈ 0.00005397319
v_b = 0.999 * (0.00005397517) + (1 – 0.999) * ((-0.06248458817) ** 2) ≈ 0.00005397319

Step 5: Calculate Bias-Corrected Estimates

Calculate bias-corrected estimates m_hat and v_hat for w and b:
m_hat_w = m_w / (1 – beta1^t) where t is the current iteration.
m_hat_b = m_b / (1 – beta1^t)
v_hat_w = v_w / (1 – beta2^t)
v_hat_b = v_b / (1 – beta2^t)
Since it’s the fourth iteration, t = 4:
m_hat_w = -1.07777865123 / (1 – 0.9^4) ≈ -1.07777865123
m_hat_b = -1.07777865123 / (1 – 0.9^4) ≈ -1.07777865123
v_hat_w = 0.00005397319 / (1 – 0.999^4) ≈ 0.00021589683
v_hat_b = 0.00005397319 / (1 – 0.999^4) ≈ 0.00021589683

Step 6: Update Parameters

Update the parameters w and b using the bias-corrected estimates and the learning rate:
w = 0.50015797537 – (0.1 / (sqrt(0.00021589683) + 1e-8)) * (-1.07777865123) ≈ 0.50017333746
b = 0.00065348285 – (0.1 / (sqrt(0.00021589683) + 1e-8)) * (-1.07777865123) ≈ 0.00066094767

Depending on the convergence criteria and the desired level of accuracy, you can either stop here or continue with more iterations to further refine the parameters w and b. The values of w and b have now been updated to approximate the best fit for the linear regression model on this dataset.

Conclusion

Adam offers advantages like adaptive learning rates, efficient exploration of the parameter space, automatic learning rate tuning, and fast convergence. However, it also presents challenges such as hyperparameter tuning, increased memory usage, sensitivity to hyperparameters, and limited generalization. Despite these limitations, Adam is a widely used optimization algorithm for training deep neural networks, especially in tasks like language generation with RNNs, due to its ability to adapt learning rates, accelerate convergence, and handle complex loss landscapes.

Let’s Work Together

StatusNeo