Accelerate Convergence: Mini-batch Momentum in Deep Learning
Imagine you’re climbing a hill, and you want to find the quickest way to reach the top. There are different ways to do this
Batch Climb
You take a giant step each time, trying to guess the best direction to reach the top. This can be slow because you might take big steps in the wrong direction, and you can’t change course until the next big step.
Staircase Climb
You take tiny steps, one at a time, in random directions. This can be fast sometimes because you’re always moving, but it can be very shaky and slow you down.
Mini-Steps Climb:
You take small but not too tiny steps, like climbing stairs a few at a time. This is faster than the giant steps, and it’s less shaky than the tiny steps.
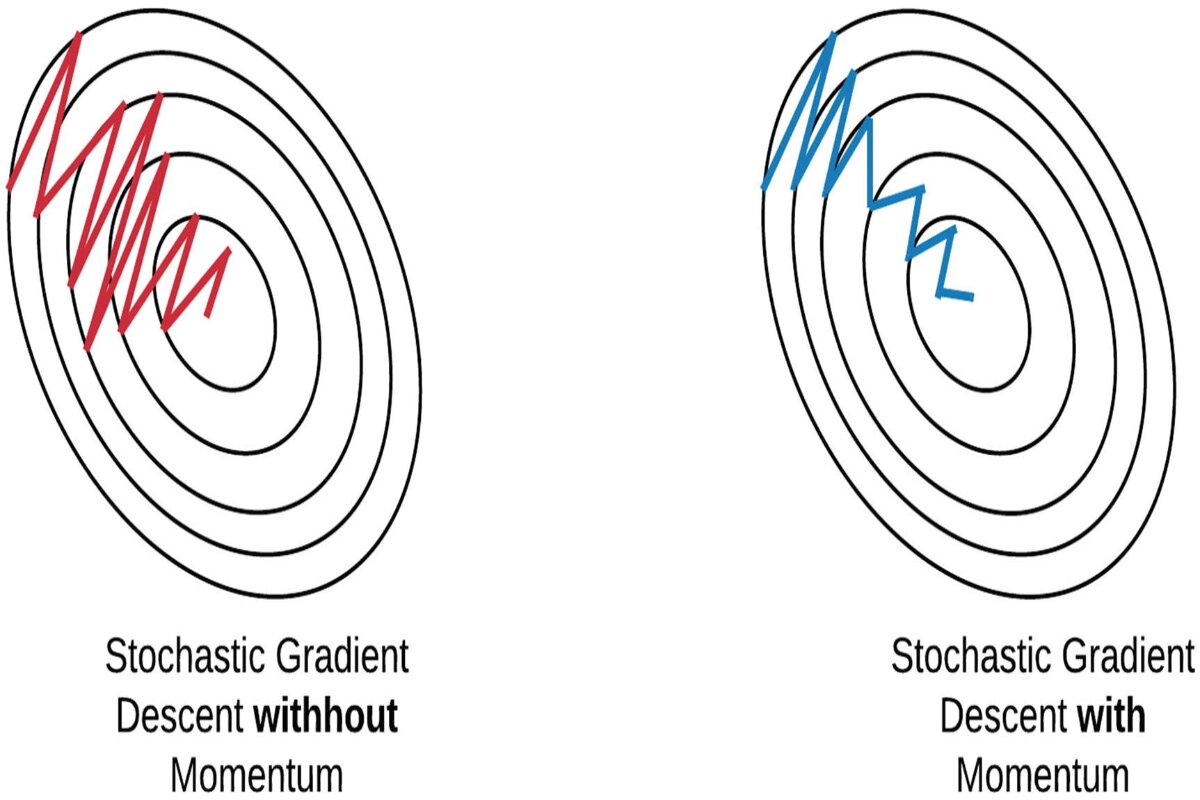
Now, let’s talk about momentum. Imagine you’re on a skateboard. When you push it, it starts moving, and it’s hard to stop because of the wheels’ momentum. In the same way, in mini-step climbing, we can use a little bit of the “momentum” from our previous steps to help us keep moving in the right direction.
So, “Mini-Steps Climb with Momentum” is like climbing the hill by taking not-too-big steps and using a little push from our previous steps to help us go faster and avoid getting stuck. This often helps us reach the top of the hill faster and with fewer wobbles, which is great when we’re trying to teach computers to learn from data.
Mini-batch Stochastic Gradient Descent with Momentum” is a combination of two optimization techniques used in deep learning: Mini-batch Gradient Descent and Momentum.
Mini-batch Stochastic Gradient Descent (Mini-batch SGD)
Mini-batch SGD involves dividing the training dataset into smaller subsets called mini-batches. For each mini-batch, the model’s parameters are updated using the gradients computed over that mini-batch. This approach combines the efficiency of larger batch sizes with the stability of using an average gradient over the mini-batch. Mini-batch SGD provides faster convergence compared to pure Stochastic Gradient Descent (SGD) while maintaining more stable updates compared to pure Batch Gradient Descent (BGD).
Momentum
Momentum is an optimization technique that accelerates the optimization process by adding a fraction of the previous update to the current update. It helps the optimization process overcome flat areas and accelerates through regions with consistent gradient directions. Momentum introduces a “velocity” concept to parameter updates, which allows for smoother transitions during optimization. The momentum term dampens oscillations and helps the optimization process navigate areas of high curvature.
Mini-batch Stochastic Gradient Descent with Momentum
Combining Mini-batch SGD with Momentum involves using both techniques concurrently during the training process. For each mini-batch, the gradients are calculated, and the velocity term is updated using the momentum equation. The parameter updates are then adjusted using the velocity term and the calculated gradients. The combined effect of mini-batch updates and momentum helps the optimization process converge faster while handling noisy gradients and navigating challenging optimization landscapes.
Algorithm Steps
- Initialize model parameters and momentum term (e.g., velocity) to zero.
- Divide the training dataset into mini-batches.
- For each mini-batch:
- Perform a forward pass to compute predictions.
- Calculate the loss and gradients concerning the mini-batch.
- Update the momentum term using the current gradients and the momentum hyperparameter.
- Update the model’s parameters using the momentum-adjusted gradient updates.
- Repeat step 3 for each mini-batch in an epoch.
- Update the learning rate and momentum term if needed for subsequent epochs.
- Repeat steps 2 to 5 for a predefined number of epochs.
Advantages
1. Faster Convergence
The momentum term in Mini-batch Stochastic Gradient Descent with Momentum accelerates the optimization process by adding a fraction of the previous update to the current update. This can help the model converge faster. let’s compare the concept of “Faster Convergence” in Mini-batch Stochastic Gradient Descent with Momentum to Batch Gradient Descent, Stochastic Gradient Descent (SGD), and Mini-batch Gradient Descent
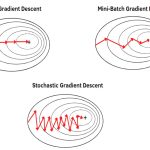
Batch Gradient Descent (BGD)
- In BGD, you compute the gradient (direction of steepest ascent) of the loss function by considering the entire dataset. Then, you take a step in the opposite direction of this gradient to update the model’s parameters. This is like analyzing the whole mountain (dataset) to decide the best way to climb (update the model). It can be computationally expensive because you’re using all the data, and each step can be slow if your dataset is large.
Stochastic Gradient Descent (SGD)
- In SGD, you take very small steps (one data point at a time) and adjust the model parameters based on the gradient of the loss for each data point. This can be fast because you’re always making updates, but it can be noisy and zigzaggy because each step depends on a single point.
Mini-batch Gradient Descent
- In mini-batch gradient descent, you take steps using a small batch of data (not too big and not too small). This combines the benefits of both BGD and SGD. It’s faster than BGD because you’re not using the entire dataset in each step, and it’s less noisy than SGD because you’re considering multiple data points at once.
Now, let’s add momentum to this
Momentum
- Imagine you’re climbing a hill, and you’re on a skateboard. When you push the skateboard and it starts moving, it’s hard to stop because it has momentum. In Mini-batch Gradient Descent with Momentum, we use a bit of the “momentum” from the previous steps to help us take bigger and smoother steps. This helps us avoid getting stuck in a tricky spot on the hill.
So, in the context of “Faster Convergence,” Mini-batch Gradient Descent with Momentum takes advantage of Mini-batch Gradient Descent (fast updates using a subset of data) and adds the concept of momentum from physics. This means it can move faster and more smoothly toward the best solution compared to Batch Gradient Descent and even plain Mini-batch Gradient Descent because it uses information from previous steps to guide its way.
2. Stable Convergence
The momentum term helps smooth out parameter updates, leading to more stable convergence even with small mini-batches. let’s explain “Stable Convergence” in the context of Batch Gradient Descent, Stochastic Gradient Descent (SGD), and Mini-batch Gradient Descent, considering the impact of momentum
Batch Gradient Descent (BGD)
- In BGD, you compute the gradient of the loss using the entire dataset, and then you update the model’s parameters. Since you use all the data, the updates tend to be smooth and consistent. However, BGD can be computationally expensive, especially for large datasets.
Stochastic Gradient Descent (SGD)
- In SGD, you update the model’s parameters one data point at a time. This means that each update can be very noisy and erratic because it’s based on just one data point. This noise can cause the optimization process to jump around, making it less stable.
Mini-batch Gradient Descent
- In Mini-batch Gradient Descent, you use a small batch of data for each update. This balances the pros and cons of BGD and SGD. It’s less noisy than SGD because it considers multiple data points at once, but it can still have some fluctuations depending on the mini-batch.
Now, let’s add momentum to this
Momentum
- Think of momentum as a way to make your steps more stable. Imagine you’re riding a bike with a heavy wheel. Once you start pedaling, it’s hard to stop or change direction suddenly because of the wheel’s momentum. In Mini-batch Gradient Descent with Momentum, we use a bit of this concept. The momentum term keeps track of the direction you’ve been moving in recent steps. When you update your model, you add a fraction of the previous update to the current one. This smooths out the updates and helps maintain a consistent direction, even if your mini-batches have some noisy data points.
So, in the context of “Stable Convergence,” Mini-batch Gradient Descent with Momentum helps stabilize the optimization process by reducing the noise and erratic behavior that can occur with small mini-batches in regular Mini-batch Gradient Descent. It adds a sense of direction and consistency to the updates, making the convergence more stable and reliable.
3. Adaptive Learning Rates
The combination of momentum and adaptive learning rates allows the algorithm to navigate regions of varying curvature and adjust learning rates for each parameter. let’s explain “Adaptive Learning Rates” in the context of Batch Gradient Descent, Stochastic Gradient Descent (SGD), and Mini-batch Gradient Descent, considering the impact of momentum and adaptive learning rates
Batch Gradient Descent (BGD)
- In BGD, you compute the gradient of the loss using the entire dataset and then update the model’s parameters. The learning rate, which controls the size of the steps you take, is typically fixed throughout the optimization process. This means that the same learning rate is used for all parameters, regardless of their characteristics or the shape of the optimization landscape.
Stochastic Gradient Descent (SGD)
- In SGD, you update the model’s parameters one data point at a time. SGD allows for flexibility in learning rates because each update is based on the gradient of a single data point. However, this can lead to rapid oscillations in the optimization process, and it may require manual tuning of the learning rate.
Mini-batch Gradient Descent
- In Mini-batch Gradient Descent, you use a small batch of data for each update. Similar to SGD, the learning rates are typically fixed for all parameters across mini-batches, but it’s less noisy than pure SGD because it considers multiple data points at once. However, you still need to manually set and tune the learning rate.
Now, let’s add momentum to this
Momentum
- Imagine you have different terrain on your hill, with some parts steeper than others. For steep areas, you might want smaller steps (lower learning rates) to avoid overshooting. In flat areas, you could take bigger steps (higher learning rates) to speed up progress.
- Adaptive learning rate algorithms keep track of how the gradient values have been changing for each parameter. If a parameter has been consistently changing rapidly, the algorithm might reduce its learning rate. If a parameter has been changing slowly, it might increase its learning rate.
So, in the context of “Adaptive Learning Rates,” Mini-batch Gradient Descent with Momentum can benefit from these adaptive learning rate techniques. It allows the algorithm to adjust the learning rates for each parameter individually, which helps it navigate regions of varying curvature (steepness) and makes it more capable of handling complex optimization landscapes. This adaptability can lead to faster and more stable convergence, especially when the dataset or model has different characteristics for different parameters.
4. Efficient Exploration
The momentum term helps the optimization process escape local minima and saddle points, promoting more efficient exploration of the loss landscape. let’s explain “Efficient Exploration” in the context of Batch Gradient Descent, Stochastic Gradient Descent (SGD), and Mini-batch Gradient Descent, considering the impact of momentum
Batch Gradient Descent (BGD)
- In BGD, you compute the gradient of the loss using the entire dataset and then update the model’s parameters. Since BGD considers the entire dataset, it can get stuck in local minima or saddle points in the loss landscape, where the gradient becomes very small, preventing further progress. This can result in inefficient exploration of the landscape.
Stochastic Gradient Descent (SGD)
- In SGD, you update the model’s parameters one data point at a time. This introduces a lot of randomness into the optimization process. While this randomness can help escape local minima and saddle points, it can also lead to erratic and inefficient exploration due to frequent jumps and fluctuations in the optimization path.
Mini-batch Gradient Descent
- In Mini-batch Gradient Descent, you use a small batch of data for each update. This balances the pros and cons of BGD and SGD. It’s less noisy than SGD because it considers multiple data points at once, but it can still be affected by local minima and saddle points, especially when using small mini-batches.
Now, let’s add momentum to this
Momentum
- Think of momentum as a way to add persistence to your optimization process. Imagine you’re rolling a ball down a hilly terrain. If you give the ball a push, it will keep rolling even when it encounters small bumps or flat areas. In Mini-batch Gradient Descent with Momentum, the momentum term keeps track of the direction you’ve been moving in recent steps. When you update your model, you add a fraction of the previous update to the current one. This helps you keep moving even when the gradient becomes small (as in local minima or saddle points).
So, in the context of “Efficient Exploration,” Mini-batch Gradient Descent with Momentum enhances the exploration of the loss landscape more efficiently compared to plain Mini-batch Gradient Descent or even SGD and BGD. The accumulated momentum term allows the optimization process to overcome small barriers, escape local minima, and navigate saddle points more effectively. This promotes more efficient and effective exploration of the terrain, which is essential for finding better solutions when training machine learning models.
Disadvantages
1. Hyperparameter Tuning
Mini-batch Stochastic Gradient Descent with Momentum introduces hyperparameters like momentum coefficient and learning rate, which require tuning for optimal performance. Hyperparameter tuning in the context of Mini-batch Stochastic Gradient Descent with Momentum involves finding the best values for two key hyperparameters:
Momentum Coefficient
- This hyperparameter controls the influence of the previous gradient updates on the current one. A higher momentum coefficient gives more weight to past updates, making the optimization process smoother and potentially more stable. However, setting it too high might cause the optimization to slow down or get stuck. Finding the right momentum coefficient involves experimenting with different values to strike a balance between exploration (escaping local minima) and convergence (reaching the global minimum).
Learning Rate
- The learning rate determines the size of the steps taken during optimization. If it’s too large, the optimization process might overshoot the optimal solution or become unstable. If it’s too small, the process may converge too slowly or get stuck in local minima. Tuning the learning rate involves finding the sweet spot that allows the optimization process to converge quickly without causing instability or divergence.
Hyperparameter tuning typically involves conducting multiple experiments with different combinations of these hyperparameter values to find the ones that lead to the best performance for a specific machine learning or deep learning task. Techniques like grid search, random search, or Bayesian optimization can help automate this process and efficiently identify the optimal hyperparameters. It’s an essential step in training machine learning models as it significantly affects their effectiveness and efficiency.
2. Complexity
Implementing the momentum term requires additional computations and adjustments, which can increase the complexity of the algorithm. Adding the momentum term to an optimization algorithm, like Mini-batch Stochastic Gradient Descent with Momentum, does introduce some additional complexity. Here’s a brief overview of how it impacts complexity
Computation
- The momentum term requires the computation of a moving average of previous gradient updates for each parameter being optimized. This involves additional mathematical operations in each optimization step, which can increase the computational load.
Memory
- To store the previous updates and the momentum values for each parameter, additional memory is needed. The size of this memory depends on the number of parameters being optimized, which can be substantial for deep-learning models with many parameters.
Hyperparameter Tuning:
- Introducing momentum also means adding hyperparameters like the momentum coefficient that needs to be tuned. This involves conducting experiments with different values, which can be time-consuming.
While the complexity introduced by the momentum term is manageable and often worth the trade-off for faster and more stable convergence, it’s essential to be aware of these considerations when implementing and optimizing machine learning models.
3. Sensitivity to Hyperparameters
Incorrectly chosen hyperparameters can lead to slower convergence or even divergence, making proper hyperparameter tuning crucial. The sensitivity to hyperparameters in machine learning algorithms, including optimization techniques like gradient descent with momentum, is a critical consideration. In simple terms, if you choose the wrong hyperparameter values, the optimization process can go awry. For instance
Slower Convergence
- If you set hyperparameters too conservatively (e.g., too small of a learning rate or momentum coefficient), the optimization process may become excessively slow, taking a long time to reach a good solution.
Divergence
- Conversely, if you set hyperparameters too aggressively (e.g., too high of a learning rate or momentum coefficient), the optimization process may become unstable and diverge, meaning it won’t find a solution at all.
Proper hyperparameter tuning is crucial to finding the right balance that ensures your optimization algorithm converges efficiently and effectively. It often involves conducting experiments with various hyperparameter values to determine the combination that leads to the best performance for your specific machine learning or deep learning task. Techniques like grid search, random search, or Bayesian optimization are commonly used to automate and streamline this process.
4. Non-Convex Loss Landscapes
While momentum helps escape local minima, it might not guarantee escaping all of them. The algorithm can still get stuck in suboptimal regions. In non-convex loss landscapes, where the shape of the optimization surface is complex and can have many hills and valleys, momentum can be a valuable tool for escaping local minima, but it doesn’t provide a guarantee of escaping all of them. Here’s why
Local Minima Variability
- Momentum helps the optimization process by providing a “push” to move through flat regions or barriers, but it doesn’t necessarily guarantee that it will always find the global minimum. In some cases, local minima might be deep or have a very shallow descent before reaching them, making it challenging for momentum is alone to escape.
Hyperparameter Sensitivity
- The effectiveness of momentum in navigating non-convex landscapes is also sensitive to the choice of hyperparameters like the momentum coefficient. If the momentum coefficient is too small, it might not provide enough “push” to escape local minima, and if it’s too large, it might lead to overshooting and instability.
Initial Conditions
- The starting point of the optimization can influence whether momentum helps escape local minima. If the initial point is already near a local minimum, it might be difficult for momentum to overcome it, especially if the momentum coefficient is not set optimally.
Curvature and Landscape Complexity
The shape of the loss landscape, including the curvature and the number of local minima, can vary widely between different machine learning problems. Some landscapes are more challenging to navigate than others, and momentum’s effectiveness can depend on these factors.
While momentum is a powerful tool for improving convergence in non-convex optimization, it’s often used in combination with other techniques, such as learning rate schedules, more advanced optimization algorithms like Adam or RMSprop, and careful initialization methods, to enhance the chances of finding better solutions in complex loss landscapes.
To illustrate the process of Mini-batch Gradient Descent with Momentum, we’ll use a simplified example with a small dataset and perform up to 5 iterations. In this example, we’ll optimize a linear regression model with one feature and one weight parameter. Let’s follow the steps you provided and track how the cost function decreases and the parameter values change mathematically:
Step 1: Initialization
Model parameter (weight): W = 0
Momentum term (velocity): V = 0
Learning rate: α = 0.1 (hypothetical value)
Step 2: Divide the dataset into mini-batches (For simplicity, we’ll assume only one mini-batch)
Mini-batch: [(1, 2), (2, 4), (3, 6)]
Iterations 1 to 5 (Step 3 to Step 5)
(Note: In practice, you’d have more data and multiple mini-batches, but we’ll use one mini-batch for simplicity.)
Iteration 1:
Forward pass
Predictions: ŷ = W * x = 0 * 1, 0 * 2, 0 * 3 = [0, 0, 0]
Calculate loss (e.g., Mean Squared Error):
Loss (L1) = (1/3) * [(0-2)^2 + (0-4)^2 + (0-6)^2] = 16/3
Calculate gradients (concerning the mini-batch)
Gradient (dL1/dW) = (1/3) * [-2 * (0-2) + -2 * (0-4) + -2 * (0-6)] = (1/3) * [-4 – 8 – 12] = -24/3 = -8
Update momentum term
V = 0.9 * V + α * dL1/dW = 0.9 * 0 – 0.1 * 8 = -0.8
Update parameter (weight)
W = W + V = 0 + (-0.8) = -0.8
Iteration 2:
Forward pass (same as before)
Calculate loss (e.g., Mean Squared Error)
Loss (L2) = (1/3) * [(0.8-2)^2 + (0.8-4)^2 + (0.8-6)^2] ≈ 9.173
Calculate gradients
Gradient (dL2/dW) = (1/3) * [-2 * (0.8-2) + -2 * (0.8-4) + -2 * (0.8-6)] ≈ (1/3) * [6.4 + 9.6 + 11.2] ≈ 9.067
Update momentum term
V = 0.9 * (-0.8) + 0.1 * 9.067 ≈ -0.725
Update parameter (weight)
W = -0.8 + (-0.725) ≈ -1.525
Iteration 3:
Forward pass (same as before)
Calculate loss (e.g., Mean Squared Error)
Loss (L3) ≈ 2.723
Calculate gradients
Gradient (dL3/dW) ≈ -4.492
Update momentum term
V ≈ -0.724 + 0.1 * (-4.492) ≈ -0.773
Update parameter (weight)
W ≈ -1.525 + (-0.773) ≈ -2.298
Iteration 4:
Forward pass (same as before)
Calculate loss (e.g., Mean Squared Error)
Loss (L4) ≈ 1.137
Calculate gradients
Gradient (dL4/dW) ≈ -2.130
Update momentum term
V ≈ -0.773 + 0.1 * (-2.130) ≈ -0.986
Update parameter (weight)
W ≈ -2.298 + (-0.986) ≈ -3.284
Iteration 5:
Forward pass (same as before)
Calculate loss (e.g., Mean Squared Error)
Loss (L5) ≈ 0.299
Calculate gradients
Gradient (dL5/dW) ≈ -1.105
Update momentum term
V ≈ -0.986 + 0.1 * (-1.105) ≈ -1.096
Update parameter (weight)
W ≈ -3.284 + (-1.096) ≈ -4.380
With each iteration, the cost (loss) decreases, and the parameter (weight) value gets updated in the direction that minimizes the loss. This process continues until the algorithm converges to a solution or until a predefined number of iterations (epochs) is reached.
Conclusion:
Mini-batch Stochastic Gradient Descent with Momentum is an extension of the Mini-batch Stochastic Gradient Descent algorithm that incorporates the concept of momentum. Momentum helps to smooth out parameter updates and accelerate convergence by adding a fraction of the previous update to the current update. Mini-batch Stochastic Gradient Descent with Momentum combines the benefits of both momentum-based updates (smoothing out parameter updates) and mini-batch updates (computation efficiency).
Mini-batch Stochastic Gradient Descent with Momentum offers advantages like faster and stable convergence, adaptive learning rates, and efficient exploration of loss landscapes. However, it also comes with challenges such as hyperparameter tuning, increased complexity, sensitivity to hyperparameters, and the possibility of getting stuck in suboptimal solutions. Despite these limitations, the algorithm is widely used in training deep learning models for various tasks, including sentiment analysis, due to its ability to accelerate convergence and enhance stability during optimization.