Why Logistic Regression For Classification Instead Linear Regression: Let’s Get It
As we know,
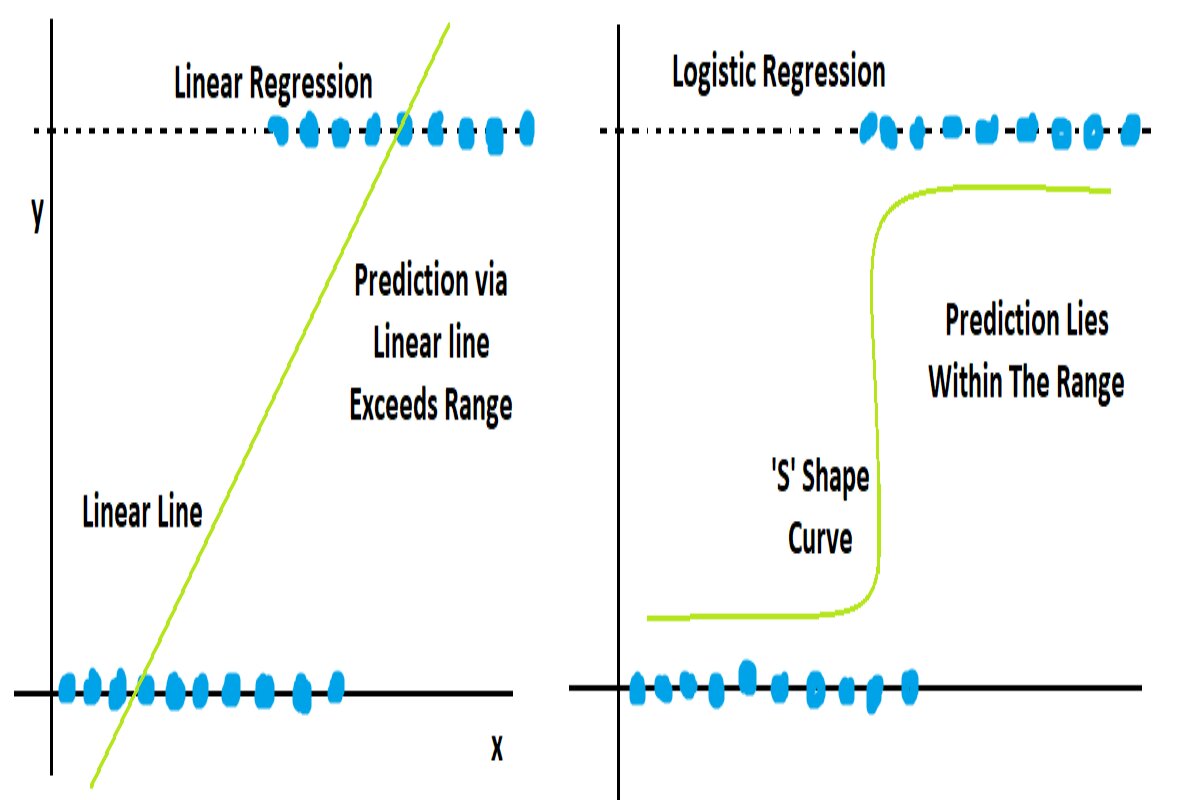
Linear Regression: It is a supervised machine learning algorithm and is used for regression-related problems where the main task is predicting the continuous values. This algorithm finds the linearity between independent variable and dependent variable. Linear regression’s prediction range is between (-∞, +∞).
Logistic Regression: It is also a type of supervised machine learning, but it can be known as a subset of linear regression. Because all the operations behind logistic regression are carried out on the basis of linear regression, But as we know, logistic regression is used for classification. Since at the time of final prediction, the logistic regression uses some log function to convert the (-∞, +∞) in 0 to 1 range.
Linear regression Find the best fit line among all the data, which will cover the maximum number of data points, and depending on this best fit line model, start to predict.
Formula : y= m*x+c
Whether
y= dependent variable
x= independent variable
m= slope
c= intercept
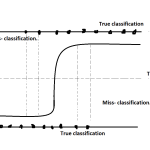
In logistic regression, model draw the “S” shape sigmoid curve which travels between 0 to 1. Just because of bound (range) between 0 & 1, there is no any possibility to draw a straight line.
Formula sigmoid σ(y) = 1 / (1 + e^(-y))
Where y = m*x+c (linear regression formula)
So now formula will be: σ(y) = 1 / (1 + e^(- m*x+c))
Now we can see some conditions by which we can conclude why not linear and why logistic
As we know, linear regression is used for continuous values, and even though we know that behind logistic regression, all operations take place on the basis of linear, still why not linear regression and why logistic?
- The first main condition of classification is range-bound, which means we need to predict between 0 and 1 only. Linear can’t predict the thing between 0 and 1, instead its range is (-∞, +∞).
- The next one is loss function. In linear regression, whatever model gets lost (errors), it comes in a large number (because operations perform on continuous values), and even if it does not, the model punishes it and increases its value just because of optimizing that loss. But in logistic regression, whatever loss is generated has a very small value. Because it’s already between 0 and 1.
- And suppose even we use linear regression for classification, while optimizing the errors derived from MSE, the model cannot get optimal updated values for parameters, and at one stage updation will stagnate. Because already classification error rates are too small, if we perform derivation with respect to MSE, the model can’t reach global minima; instead, it reaches local minima, and the problem of gradient vanishing happens.
- The next reason is data. While predicting the class (let’s assume here for binary classification), there are only two classes, and there is a possibility that whatever independent variables are there, we can find some similarities between them, so this condition violates the assumption of linear regression, which is independence; There shouldn’t be dependency between independent variables.
- The next reason is linearity. There is no possibility that we could find the linear relationship between independent and dependent variables for classification. Because in classification there are possibilities of similarity in independent variables,
- Linear regression doesn’t allow multicollinearity, but logistic regression does to a lesser extent.
- Data is divided into two classes that are not compatible for linear to perform the operation.
Now let’s see what the differences are between them.
| Linear Regression | Logistic Regression |
| Use for regression | Use for classification |
| Two types: 1. Simple Linear Regression 2. Multiple Linear Regression | Two Types: 1. Binary Classification 2. Multiclass Classification |
| Range between (-∞, +∞) | Range between 0 to 1 |
| Loss Function: MSE = (1/n) * Σ(yᵢ – ȳ)² | Loss Function: Log Loss= -(1/n) * Σ[yᵢ * log(ŷᵢ) + (1 – yᵢ) * log(1 – ŷᵢ)] |
| There is no threshold for output or result | Threshold for predicting the class. By default, 0.5 is the threshold |
| Sensitive to Outliers | Robust to Outliers |
| Evaluation parameter: SSE, MSE, MAE, R2 Score, Adjusted R2 Score | Evaluation Parameter: Log Loss, Precision, Recall, Accuracy Score, F1 Score |
| Handle Multiple Targets | Handle Multiple Classes |
| The model is simple, with only a few features | The model is complex, and its dimensionality is also high |
| Output might be a new value or nearby | Output is always similar because of discrete values |
| Linearity: Independent variables and output variables should linearly depend | Logistic regression cannot require such linearity between independent and dependent variables |
| Dependency: There shouldn’t be a dependency between independent variables | Logistic allows dependency between independent variables. |
| In linear regression, while updating the parameter values, the model gets only global minima | In logistic regression, while updating parameters, the model will get few local minima and finally the global minima |
| Missing data can be easily handled. Because data is found in continuous format and since we can overcome missing data by using the mean value | Missing data should be handled very carefully because if wrong imputation takes place, we get biased probabilities |
| Linear regression does not find confidence in output or result, because it predict the continuous value. | Logistic regression Find the confidence ratio of that probability by using the likelihood estimation function |
| Linear regression is a highly interpretable algorithm. | Logistic regression is not a very interpretable model |
| Linear regression could predict the output beyond its target value | Logistic regression only predicts within the range of the target variable |
| Get Normally distributed data | Get binomial distribution of data |
| Linear regression requires one hot encoding to handle multiclass categorical variables | Logistic can easily handle the multiclass categories variable without one hot encoding |
| Linear regression is used for both Univariate and multivariate analyses | Logistic, due to classification, uses only multivariate |
| Linear regression is formulated as a minimization problem to find the best-fitting line that reduces the prediction error | Logistic regression is formulated as a maximum likelihood estimation problem to find the parameters that maximise the likelihood of the data given the model |
| Applications: predicting sales, housing prices, or any continuous numeric value | Applications: classification tasks, where there are only two classes (e.g., yes/no, true/false) |