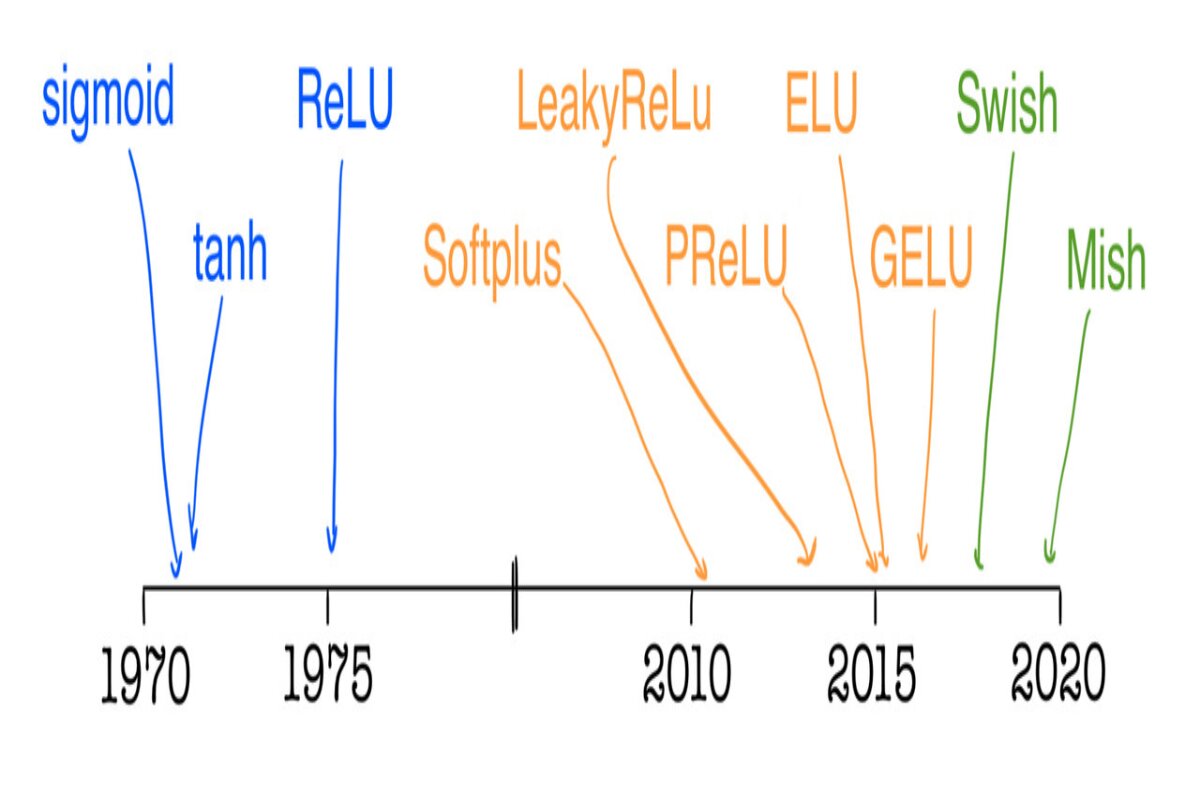
Mastering Activation Functions: Unleashing Neural Power
Activation Function:
At the heart of artificial neural networks, an activation function plays a crucial role in introducing non-linearity to the model, enabling it to capture complex relationships within data. Starting from a simple understanding and delving into a deeper explanation, let’s explore the concept of an activation function.
Imagine a neural network as a computational model inspired by the human brain. It consists of interconnected nodes, called neurons, organized into layers. Each connection has a weight that adjusts during training. Neurons receive inputs, process them, and generate outputs. However, without introducing non-linearity, the network would be limited to linear transformations, which can’t capture intricate patterns in data.
Here are some hints that might lead to choosing activation functions:
Non-Linearity in Data
- When the relationship between inputs and outputs is inherently non-linear, linear models (without Activation Function used models) would struggle to capture these complex patterns. Activation functions enable neural networks to represent such non-linear relationships effectively.
Hierarchical Features
- Many real-world problems involve hierarchical features that interact in non-linear ways. Activation functions help neural networks learn these intricate interactions, whereas linear models (without Activation Function used models) would fail to capture the depth and complexity of such relationships.
Complex Decision Boundaries
- Tasks that require complex decision boundaries to separate different classes often demand non-linear models (with Activation function-used models). Activation functions allow neural networks to create intricate decision boundaries, critical for tasks like image recognition, object detection, and natural language processing.
Capturing Variability
- In situations where data exhibits variability that cannot be well-approximated by linear relationships (without Activation Function used models), activation functions come into play. They help neural networks model and capture the diverse variations present in the data.
Data Transformation
- When the input data needs to be transformed into a different representation that involves non-linear operations, activation functions are essential. For example, transforming raw pixel values of an image into meaningful features for image classification requires non-linearity.
Feature Engineering Complexity
- Some problems require complex feature engineering to reveal meaningful patterns. Activation functions can automatically learn and extract such features from raw data, reducing the need for extensive manual feature engineering.
Sequential and Temporal Data
- Tasks involving sequences, time series, or temporal relationships inherently demand non-linear models (with Activation Function used models). Activation functions are crucial for capturing the evolving patterns over time.
Handling Multimodal Data
- When data exhibits multiple modes or clusters, linear models might struggle to differentiate between these modes. Activation functions enable neural networks to distinguish between complex data distributions.
Addressing the Vanishing Gradient Problem
- Activation functions like ReLU, Leaky ReLU, and their variants help alleviate the vanishing gradient problem in deep networks. This is particularly important when working with architectures involving numerous layers.
Learning Representations
- Activation functions contribute to learning meaningful representations of data. This is valuable in tasks like transfer learning, where the network should capture generic features from one domain to apply to another.
Tend to opt for activation functions over linear models (without Activation Function used models) when dealing with complex, non-linear problems that involve intricate patterns, hierarchical features, and complex decision boundaries. Activation functions empower neural networks to effectively capture and model the richness of real-world data.
That’s why the activation function steps in. It adds a non-linear element to each neuron’s output, enabling the network to approximate more complex relationships, crucial for tasks like image recognition, language processing, and more. As we see earlier activation function determines the output of a neuron given its inputs and weights It decides whether the neuron should “fire” or not based on the weighted sum of inputs. The output of an activation function then serves as input for the next layer of neurons.
What Happens if Activation Functions are Not Used?
If activation functions are not used in a neural network, the network’s behavior would be limited to linear transformations.
This has several significant implications:
Limited Expressiveness
- The network would only be able to learn linear transformations of the input data. It wouldn’t be able to capture complex patterns, intricate relationships, or hierarchical features present in real-world data.
Inability to Solve Complex Tasks
- Many real-world problems require the network to learn and represent nonlinear relationships. Without activation functions, the network would struggle to solve tasks that involve recognizing objects in images, understanding natural language, making predictions based on historical data, and more.
Shallow Representations
- The network’s ability to represent data and extract meaningful features would be limited. Deeper layers wouldn’t provide any advantage over shallow layers since stacking linear operations doesn’t lead to increased representation capacity.
Lack of Learning Capacity
- Neural networks with linear transformations would lack the learning capacity needed for many challenging tasks. The network’s ability to generalize and adapt to diverse inputs would be severely compromised.
Activation functions are essential for allowing neural networks to model complex relationships, learn intricate patterns, and solve a wide range of tasks. Without activation functions, neural networks would lose their ability to capture non-linearity, leading to limited representation capacity and an inability to handle complex real-world problems effectively.
How Idea comes to use activation function, the idea comes after studying the human brain. how the Activation Function works similarly to the human brain. Let’s see
Non-Linearity
- Just as activation functions introduce non-linearity in neural networks, biological neurons also exhibit non-linear behavior. In the brain, the firing of a neuron is not a linear response to input stimuli; instead, there is a threshold that needs to be exceeded before a neuron “fires” or becomes active. This non-linear response allows for the brain to process complex information and recognize intricate patterns.
Threshold Activation
- Activation functions like ReLU, Leaky ReLU, and sigmoid mimic the threshold activation behavior of biological neurons. In the brain, neurons remain relatively inactive until they receive a certain level of stimulation, surpassing a threshold. Similarly, in neural networks, activation functions ensure that neurons don’t activate until the input reaches a certain threshold or level.
Signal Propagation
- In neural networks, the output of one layer of neurons serves as input to the next layer. Similarly, in the brain, when a neuron fires, it sends electrical signals (action potentials) to connected neurons, influencing their behavior. This parallel emphasizes the idea of signal propagation and information flow through interconnected units.
Complex Representation
- Activation functions in neural networks enable the learning of complex representations of data. In the brain, different patterns of neural firing are associated with different concepts, memories, or perceptions. Similarly, the non-linear behavior introduced by activation functions allows neural networks to learn and represent intricate relationships between inputs and outputs.
Adaptation and Learning
- Just as neural networks adjust weights during training to improve performance, synapses in the brain strengthen or weaken based on learning and experience. Activation functions facilitate learning by controlling how much a neuron should respond to input changes, aiding the network’s adaptation to different patterns.
Diversity of Activation Responses
In neural networks, different activation functions have distinct response curves. Similarly, different types of neurons in the brain have varying thresholds, excitabilities, and response patterns. This diversity allows both networks to process and interpret various types of information.
It’s important to note that while there are parallels between activation functions and biological neurons, artificial neural networks are a simplified abstraction inspired by the brain’s behavior. Real neurons are vastly more complex and operate with a multitude of biochemical processes that extend beyond the mathematical equations governing activation functions. Nonetheless, the concept of introducing non-linearity, threshold behavior, and complex representation remains a bridge between artificial neural networks and the intricate behavior of the human brain.
Applying activation functions in neural networks offers several benefits, enabling them to effectively model complex relationships, capture intricate patterns, and tackle a wide range of challenging tasks.
Here are the key benefits of using activation functions:
Non-Linearity
- Activation functions introduce non-linearity to neural networks, allowing researchers to capture and represent complex, non-linear relationships in data. This is crucial for solving real-world problems that involve intricate patterns and interactions.
Expressive Power
- Activation functions enhance the expressive power of neural networks. Researchers can model a diverse range of functions and behaviors, making neural networks versatile tools for various domains, including image processing, natural language understanding, and more.
Feature Extraction
- Activation functions enable neural networks to automatically extract meaningful features from raw data. Researchers don’t need to manually engineer features, saving time and effort while improving performance.
Learning Hierarchical Representations
- Neural networks with activation functions can learn hierarchical representations of data. They can capture complex hierarchical features and relationships, providing a deeper understanding of the underlying structures in the data.
Handling Complex Decision Boundaries
- Activation functions allow neural networks to create intricate decision boundaries that can separate complex classes in tasks like image classification, object detection, and segmentation.
Adaptation to Data
- Activation functions help neural networks adapt to the specific characteristics of the dataset. They can learn from the data to determine the best non-linear transformations that lead to improved accuracy and generalization.
Improved Learning Dynamics
- Activation functions like ReLU and its variants mitigate the vanishing gradient problem, enabling more stable and faster training of deep networks. This accelerates convergence and facilitates the training of deeper architectures.
Enhanced Generalization
- Activation functions contribute to improved generalization capabilities of neural networks. They help networks generalize learned patterns to unseen data, resulting in better performance on new instances.
Multimodal and Temporal Data
- Activation functions are essential for modeling multimodal data and handling sequential and temporal relationships. They enable researchers to process and understand data with different modes and time-dependent patterns.
Innovation and Research Exploration
- Activation functions provide researchers with a canvas to explore new ideas and innovations. Experimenting with different activation functions can lead to novel network architectures and improved performance.
Problem-Solving Flexibility
- Different activation functions suit different problem domains. Researchers can choose the activation function that best aligns with the characteristics of the data and the requirements of the task.
Staying Current
- With ongoing research and development, new activation functions are being proposed that address specific challenges. Researchers can stay up-to-date and incorporate the latest advancements to enhance their models.
Applying activation functions empowers to creation of more powerful, adaptable, and efficient neural network models. These functions enable the network to capture complex patterns, solve challenging problems, and provide a deeper understanding of data. Activation functions play a crucial role in the success of neural network research across a wide spectrum of domains.
There are various activation functions, each with distinct characteristics:
Sigmoid Activation Function

The Sigmoid activation function is a mathematical function used in neural networks to introduce non-linearity into the network’s computations. It takes an input value ‘x’ and maps it to an output value between 0 and 1.
Formula
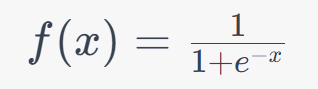
Here, ‘e’ represents the mathematical constant approximately equal to 2.71828
If the value of z goes up to positive infinity, then the predicted value of y will become 1. But if the value of z goes down to negative infinity, then the predicted value of y will become 0.
Range
The Sigmoid function squashes its input to a range between 0 and 1. This means that no matter how large or small the input ‘x’ is, the output of the Sigmoid function will always fall within the range (0, 1). As a result, it’s often used to produce probabilities or binary outcomes, such as in logistic regression or binary classification problems.
Usefulness and How It Works
The Sigmoid function was historically popular because it converts any input into a value that can be interpreted as a probability. This makes it useful for tasks like binary classification, where you want the output to represent the probability of belonging to a particular class.
For example, let’s say you have a binary classification problem where you’re trying to determine whether an email is spam or not. The output of your neural network needs to indicate the probability that the email is spam. By using the Sigmoid activation function in the final layer of your network, you can ensure that the output is between 0 and 1, which can be directly interpreted as the probability of being spam.
Issues – Vanishing Gradient
However, the Sigmoid function has a significant drawback known as the vanishing gradient problem. When the input to the Sigmoid function is very large or very small, the slope of the function becomes very flat. This means that during backpropagation (the process of updating the neural network’s weights), the gradients can become extremely small. Small gradients can lead to slow convergence during training and can even cause the network to stop learning effectively.
Due to this vanishing gradient issue, the Sigmoid function has fallen out of favor in many deep-learning architectures. Activation functions like ReLU (Rectified Linear Unit) and its variants have gained popularity because they do not suffer from the vanishing gradient problem to the same extent.
The sigmoid activation function was historically useful for its ability to provide probabilistic outputs, but its vanishing gradient problem has led to its decreased usage in modern deep-learning architectures.
Hyperbolic Tangent (tanh) Activation Function

The Hyperbolic Tangent (tanh) activation function is another nonlinear function commonly used in neural networks. It’s similar to the Sigmoid function but is centered around 0 and has a range between -1 and 1.
Formula
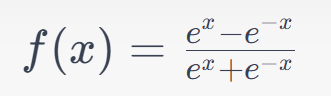
Here, ‘e’ represents the mathematical constant approximately equal to 2.71828
Range and Centering
The tanh function squashes its input to a range between -1 and 1. Unlike the Sigmoid function that squashes input between 0 and 1, the tanh function allows negative values as well. This means that the tanh function produces both positive and negative outputs while being centered around 0. This centered behavior makes it more suitable for some types of data preprocessing.
Usefulness and How It Works
The tanh function is useful for tasks where the data ranges from negative to positive values. It’s often used in situations where the output of a neural network needs to be both positive and negative, for instance, in image classification where pixel values can be both brighter (positive) and darker (negative).
For example, consider an image classification task where you’re training a neural network to classify grayscale images of handwritten digits into different classes (0-9). The pixel values in the images range from 0 (black) to 255 (white). By using the tanh activation function, the network can model both positive and negative variations in pixel intensity, allowing it to capture subtle features in the images that differentiate between different digits.
The centered nature of tanh also means that the average output of the neurons will be close to zero, which can help with convergence during training. It mitigates the vanishing gradient problem to some extent compared to the Sigmoid function. However, similar to the Sigmoid function, Tanh can still suffer from the vanishing gradient problem when inputs are extremely large or small, which can slow down the training process. The tanh activation function is useful when dealing with data that has both positive and negative values. Its centered behavior around zero makes it appropriate for tasks where the output needs to capture variations in both directions.
While it has some advantages over the Sigmoid function, it still has limitations like the vanishing gradient problem, which has led to the adoption of alternative activation functions like ReLU and its variants in many modern architectures.
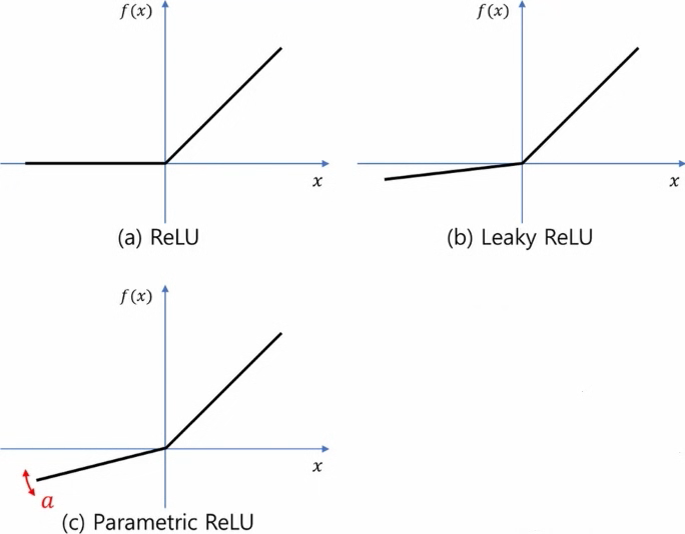
Rectified Linear Unit (ReLU) Activation Function
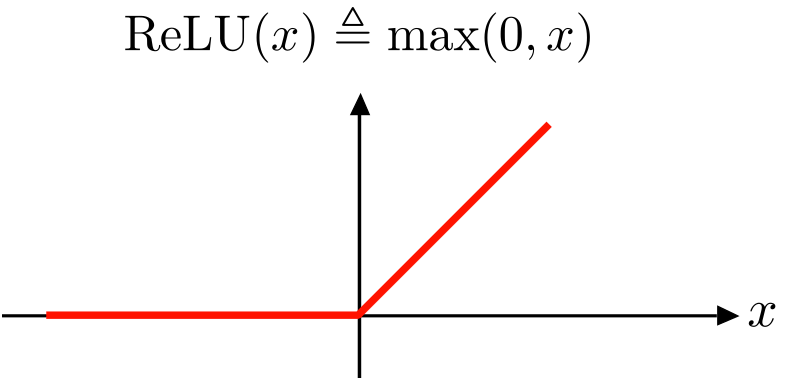
The Rectified Linear Unit (ReLU) is one of the most popular activation functions in deep learning. It’s simple but highly effective.
Formula

In this formula, the function takes the input ‘x’ and returns ‘x’ if ‘x’ is positive, and returns 0 if ‘x’ is negative.
Range
The ReLU function outputs 0 for any negative input and retains the positive input as is. This means that the range of the ReLU function is [0, +∞), which implies that the function does not impose an upper limit on the output. This unbounded positive output is a key characteristic of the ReLU activation function.
ReLU function and its derivative are monotonic. If the function receives any negative input, it returns 0; however, if the function receives any positive value x, it returns that value. As a result, the output has a range of 0 to infinite.
Usefulness and How It Works
The ReLU activation function is incredibly useful due to its simplicity and its ability to mitigate the vanishing gradient problem. The vanishing gradient problem occurs when gradients during backpropagation become very small, leading to slow or halted learning. ReLU addresses this by allowing positive gradients to pass unchanged, thus avoiding the vanishing gradient issue that is prominent in activation functions like Sigmoid and tanh.
For example, consider an image classification task. Each neuron in a neural network layer processes a weighted sum of inputs. Applying ReLU to the output of each neuron will replace all negative values with zeros, effectively introducing a non-linearity while maintaining a simple and efficient computation. This allows the network to learn and adapt to complex patterns in the data.
The unbounded positive range of ReLU can also enhance learning efficiency. Neurons can develop large, positive outputs, which can speed up convergence during training. However, this unbounded nature can also lead to another issue called the “dying ReLU” problem, where neurons can become inactive (output 0) for all inputs during training, essentially stopping them from learning. This is where variants of ReLU like Leaky ReLU and Parametric ReLU come in, which allow small, non-zero outputs for negative inputs to avoid the dying ReLU problem.
ReLU is useful due to its simplicity and effectiveness in addressing the vanishing gradient problem, which can hinder the training of deep networks. Its output range, particularly the absence of an upper limit, contributes to faster convergence and efficient learning. Despite its benefits, it’s important to consider variants like Leaky ReLU in scenarios where the “dying ReLU” problem might occur.
Leaky Rectified Linear Unit (Leaky ReLU) Activation Function

The Leaky Rectified Linear Unit (Leaky ReLU) is a variation of the standard ReLU activation function. It’s designed to address the “dying ReLU” problem that can occur with the standard ReLU function.
Formula
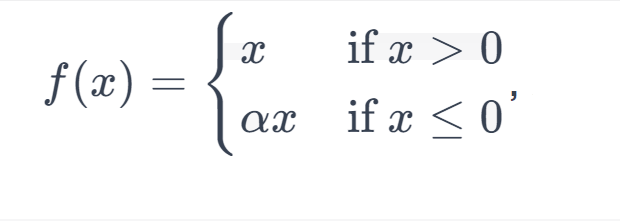
Here, ‘a’ is a small positive constant that is usually chosen to be a small value like 0.01.
Range
The range of the Leaky ReLU function is from negative infinity to positive infinity, similar to the ReLU function.
This function returns x if it receives any positive input, but for any negative value of x, it returns a really small value which is 0.01 times x. Thus it gives an output for negative values as well.
Usefulness and How It Works
The Leaky ReLU activation function is useful because it addresses a limitation of the standard ReLU function, known as the “dying ReLU” problem. The dying ReLU problem occurs when a neuron’s output becomes negative and remains negative for all inputs, causing the neuron to become inactive (outputting 0) and effectively stopping it from learning. This happens because the gradients for negative inputs are always zero in the standard ReLU function.
Leaky ReLU addresses this by allowing small negative outputs for negative inputs. The parameter ‘a’ introduces a small slope for negative inputs, which means that even if the input is negative, the neuron will still have a non-zero gradient and can potentially update its weights during backpropagation.
For example, imagine training a neural network for image classification. A certain neuron in the network might be responsible for detecting certain features in images. If the standard ReLU is used, and the weights are such that this neuron consistently receives negative inputs, it might become inactive and stop learning. By using Leaky ReLU, even small negative inputs can contribute to the neuron’s learning process, potentially preventing it from becoming inactive.
Leaky ReLU is useful because it addresses the “dying ReLU” problem by allowing small gradients for negative inputs, thus enabling neurons to continue learning even when they receive negative inputs. The small, non-zero gradient for negative inputs helps to overcome the issue of inactive neurons that can occur with the standard ReLU function. While Leaky ReLU is effective in preventing neurons from dying, it’s worth noting that there are other variants like Parametric ReLU (PReLU) where the ‘a’ parameter can also be learned during training.
Parametric Rectified Linear Unit (PReLU) Activation Function
The Parametric Rectified Linear Unit (PReLU) is an extension of the Leaky ReLU activation function. In Leaky ReLU, the parameter determines the slope for negative inputs. In PReLU, this parameter is not a fixed constant; instead, it’s learned during the training process, making it a trainable parameter.
Formula
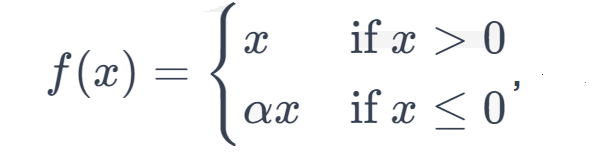
Here, ‘a’ is a learned parameter that the network adjusts during the training.
Usefulness and How It Works
PReLU is useful because it combines the benefits of Leaky ReLU (preventing the “dying ReLU” problem by allowing small gradients for negative inputs) with the capability to adaptively learn the parameter ‘a’ for each neuron during training.
The major advantage of using a learnable parameter ‘a’ is that the network can determine the optimal slope for negative inputs on its own. This can lead to improved performance, as different neurons in the network might need different slopes to better model the data
Let’s consider a simple example involving image classification using a neural network. Suppose we’re building a network to classify animals, and one of the neurons in a hidden layer is responsible for recognizing features related to fur. Some animals might have very distinct fur patterns, while others might have subtle variations. By using PReLU for this neuron, the network can learn the most suitable slope ‘a’ for negative inputs. If some animals’ fur patterns are better captured with a steeper slope, the network can adapt and learn that during training. Similarly, if some animals’ fur patterns are better captured with a gentler slope, the network can adjust it accordingly. This adaptability can lead to a more efficient and accurate learning process.
PReLU is useful because it combines the flexibility of Leaky ReLU (preventing the “dying ReLU” problem) with the capability to learn the slope parameter ‘a’ during training. This adaptability allows the network to better model complex patterns in the data and potentially leads to improved performance compared to fixed-slope activation functions.
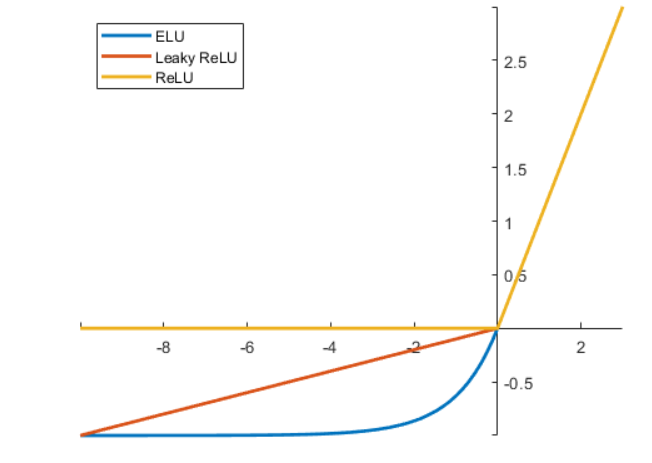
Exponential Linear Unit (ELU) Activation Function

The Exponential Linear Unit (ELU) is a type of activation function that aims to overcome some of the limitations of the ReLU family of functions while maintaining their benefits.
Formula

Here, ‘a’ is a small positive constant and e represents the mathematical constant approximately equal to 2.71828
Purpose and How It Works
The ELU activation function is designed to address two main issues associated with the ReLU family of functions: dead neurons and negative outputs for negative inputs.
Dead Neurons
In the standard ReLU activation function, neurons can become “dead” when they always output zero for negative inputs, essentially stopping the learning process for those neurons. ELU helps alleviate this by having a non-zero gradient for negative inputs, which means neurons are less likely to become inactive during training.
Negative Outputs for Negative Inputs
Some activation functions like ReLU and its variants can produce negative outputs for negative inputs, which might not always be desired, especially when dealing with certain data distributions.
Usefulness
ELU is useful because it helps in preventing dead neurons and produces smoother gradients for both positive and negative inputs. Let’s consider an example of training a neural network for image denoising. The network’s task is to remove noise from noisy images.
For this task, the network must handle both positive and negative pixel values in the image. Using ReLU in this scenario could lead to some neurons becoming inactive for negative inputs, causing them to not contribute to the denoising process. Additionally, ReLU could produce negative denoised pixel values, which might not be physically meaningful. By using the ELU activation function, the network can maintain non-zero gradients for negative inputs, ensuring that all neurons contribute to the denoising process. Also, ELU’s formula ensures that the outputs remain positive or close to zero for negative inputs, preserving the meaning of pixel values in the context of image denoising.
The Exponential Linear Unit (ELU) activation function is useful because it helps prevent dead neurons and produces smoother gradients for both positive and negative inputs. By introducing a saturation point and a non-zero gradient for negative inputs, ELU addresses issues that can arise with other activation functions like ReLU and its variants. This makes ELU particularly suitable for scenarios where negative inputs and their corresponding outputs need to be handled more effectively.
Swish Activation Function
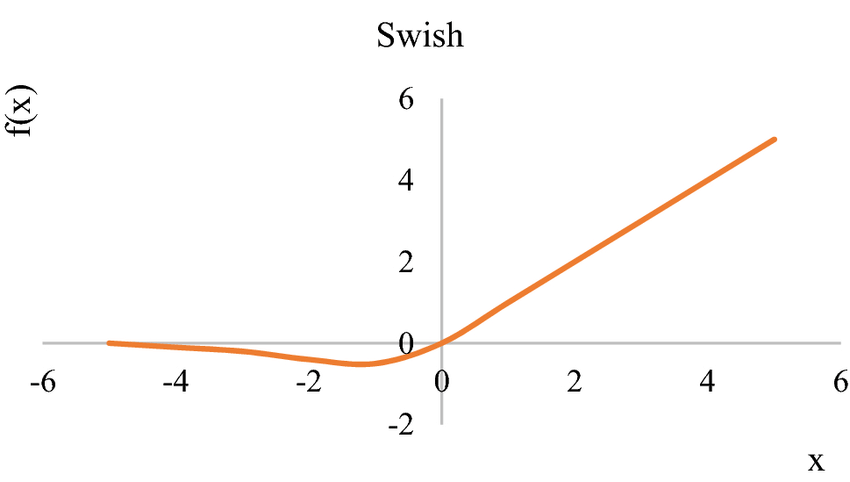
The Swish activation function is a relatively new addition to the family of activation functions used in deep learning. It’s designed to offer an alternative to the ReLU activation function with a smoother behavior.
Formula
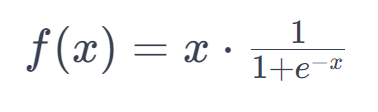
Range and Smooth Behavior
Swish activation is used in the Long Short-Term Memory (LTST) neural networks, which are used extensively in sequence prediction and likelihood problems.
Usefulness and How It Works
The Swish activation function was proposed as an alternative to ReLU to address some of the limitations that ReLU can exhibit, such as the “dying ReLU” problem and the potential for large positive outputs.
Advantages over ReLU
Smoother Transition: The sigmoid component of the Swish function provides a more gradual transition from the negative side to the positive side, which can help avoid the abrupt switch that ReLU has. This can lead to a more stable and smooth learning process.
Non-Monotonicity: Unlike ReLU, which is a piecewise linear function, Swish has a non-monotonic shape. This can allow the function to capture more complex patterns in the data and potentially improve the representation power of the network.

Consider a neural network designed for sentiment analysis, where the task is to determine the sentiment (positive, negative, neutral) of a given text. For certain sentences, the sentiment might not be immediately clear based on individual words, and the network needs to capture more subtle patterns.
Using Swish in this scenario could help the network capture these subtleties due to its non-monotonic nature and smoother transition around zero. This can be particularly beneficial when dealing with nuanced language and complex relationships between words.
The Swish activation function is useful as an alternative to ReLU, offering a smoother behavior and the potential to capture more complex patterns in data. Its characteristics can be advantageous for tasks that require capturing subtle patterns and relationships in the data, making it an interesting choice for various applications in deep learning.
Scaled Exponential Linear Unit (SELU) Activation Function
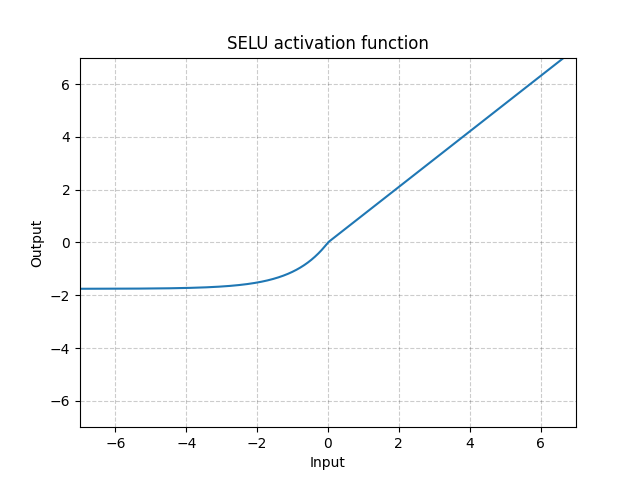
The Scaled Exponential Linear Unit (SELU) is an activation function designed to address challenges like vanishing and exploding gradients in deep neural networks. It’s an extension of the Exponential Linear Unit (ELU) activation function.
Formula
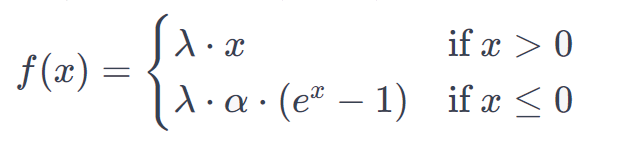
where alpha and lambda are pre-defined constants (alpha=1.67326324 and lambda=1.05070098).
Purpose and How it Works
The primary purpose of the SELU activation function is to encourage self-normalization in deep neural networks. Self-normalization means that the activations of each layer have a stable mean and variance during both forward and backward passes, which helps alleviate the vanishing and exploding gradient problems.
How it Works
- 1. The lambda parameter is chosen such that it maintains the mean of the activations close to 0 and the standard deviation close to 1 during the forward pass.
- 2. The parameter alpha governs the slope of the function for negative inputs, similar to the ELU activation function.
- 3. The specific choices of lambda and alpha help ensure that the activations neither explode (increase rapidly) nor vanish (decrease rapidly) as they are propagated through the layers during training.
Usefulness
Imagine training a deep neural network for image recognition, where the network consists of many layers processing intricate patterns within images. As the network becomes deeper, traditional activation functions might cause gradients to vanish, making training slow and difficult.

By using the SELU activation function, the network can maintain more stable gradients, enabling faster convergence. For instance, in object detection tasks, the network can learn to recognize objects even when they appear in different scales, angles, and lighting conditions, thanks to SELU’s self-normalization property.
The Scaled Exponential Linear Unit (SELU) activation function is valuable for deep neural networks because it encourages self-normalization, addressing issues like vanishing and exploding gradients. Its carefully chosen scaling parameters help maintain stable statistics within layers, allowing for more efficient and effective training of deep architectures. SELU can be particularly advantageous when working with very deep networks in various domains such as computer vision, natural language processing, and more.
Mish Activation Function
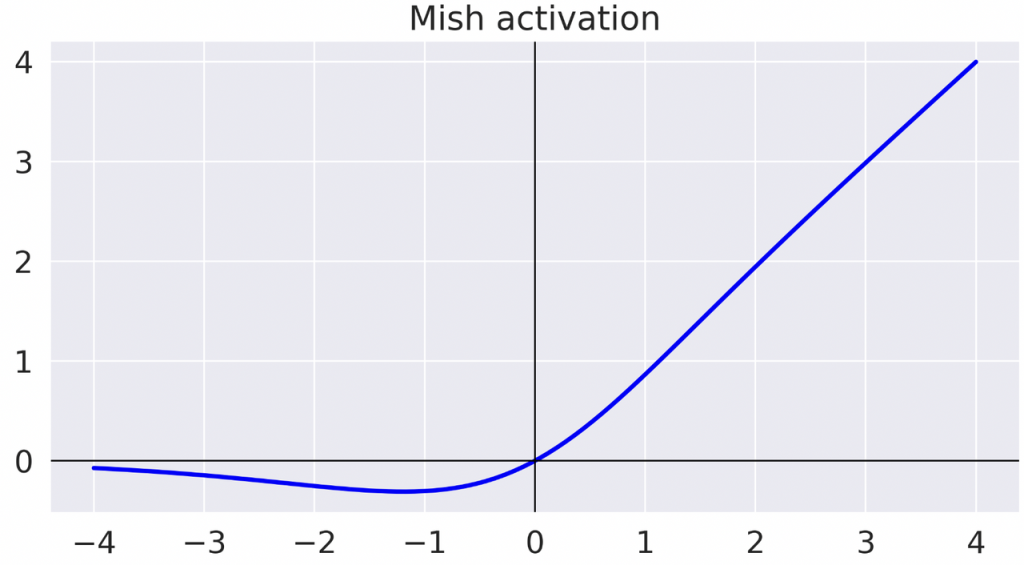
The Mish activation function is another novel addition to the family of activation functions used in deep learning. It’s designed to provide an alternative to existing activation functions like Swish and ReLU.
Formula
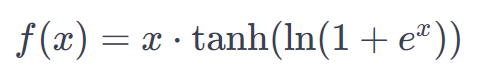
Here, ‘tanh’ is the hyperbolic tangent function and e represents the mathematical constant approximately equal to 271828.
Range and Behavior
The Mish activation function has a similar range to ReLU and Swish, which is (−∞,+∞). It introduces a smooth curve that is steeper in the center than ReLU and Swish, and it tapers off gently towards both ends.
Usefulness and How it Works
The Mish activation function was introduced as a potential improvement over existing functions like Swish, aiming to provide better performance on certain tasks. Its unique curve shape combines the advantages of both ReLU and Swish functions while avoiding some of their drawbacks.
Potential Advantages
Non-Monotonicity: Like Swish, Mish is non-monotonic, meaning its shape isn’t strictly increasing or decreasing. This characteristic can enable the function to capture complex relationships in the data.
Smoothness and Gradient Flow
The smoothness of the Mish function and its controlled gradient flow can contribute to a more stable training process and potentially faster convergence.
Reduced Risk of Dead Neurons
Mish, like Swish, may reduce the risk of “dying neurons” compared to standard ReLU. The gentle tapering-off behavior at both ends of the curve ensures that even very negative inputs receive some gradient during backpropagation.

Let’s consider an example of an image classification task where you’re training a convolutional neural network (CNN) to classify different species of flowers based on images. The network needs to detect intricate features like petal patterns and colors.
In this scenario, the Mish activation function could be beneficial due to its non-monotonic behavior and smoothness. The function’s curve could help the network better capture the diverse and sometimes subtle variations in petal patterns and colors, leading to improved classification accuracy.
The Mish activation function is useful as an alternative to existing activation functions, offering a combination of advantages from ReLU and Swish. Its unique curve shape aims to provide better performance on certain tasks by capturing complex patterns in the data, maintaining smoothness, and addressing potential issues like “dying neurons.” While it’s relatively new and its benefits are still being explored, it presents an interesting option for experimentation in various deep-learning tasks.
Softmax Activation Function

The Softmax activation function is commonly used in the output layer of a neural network for multi-class classification tasks. It converts raw scores, also known as logits, into probability distributions over multiple classes.
Formula

Usefulness and How It Works
The Softmax activation function is incredibly useful for multi-class classification tasks, where an input needs to be classified into one of several possible classes. It transforms the raw scores into a probability distribution, indicating the likelihood of the input belonging to each class
Let’s consider an example of a neural network for classifying handwritten digits into one of ten possible classes (0 to 9). The network takes an image of a digit as input and produces raw scores for each class. For instance, an image might receive the following raw scores: [2.1, -1.5, 0.8, 3.6, -0.2, 5.0, 1.3, -2.0, 0.1, 2.8].
Applying the Softmax function to these raw scores will convert them into probabilities. After applying Softmax, the scores might become: [0.045, 0.004, 0.018, 0.215, 0.009, 0.629, 0.027, 0.002, 0.013, 0.038]. Here, class 5 has the highest probability (0.629), indicating that the network predicts the input image as class 5 (digit 5) with the highest confidence.
The Softmax activation function is a crucial tool for multi-class classification tasks in deep learning. It converts raw scores into meaningful probability distributions, allowing the network to make confident predictions about the most likely class for a given input. Softmax enables the network to provide clear and interpretable results for tasks that involve choosing one class out of many possible classes.
Gated Linear Unit (GLU) Activation Function
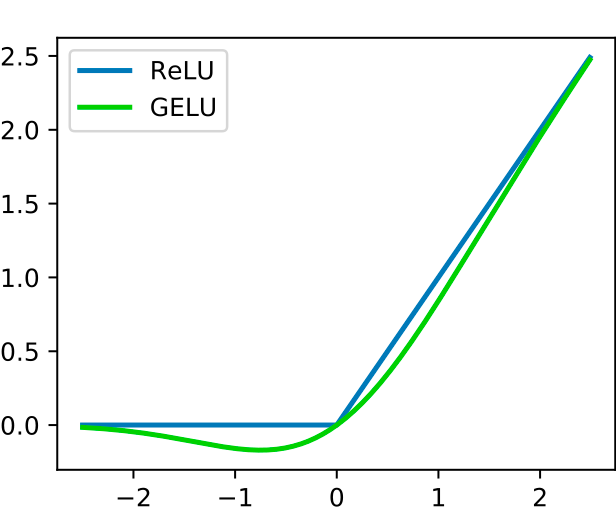
The Gated Linear Unit (GLU) is a specialized activation function that is used in some architectures, particularly in sequence-to-sequence tasks like language translation and text generation. It involves splitting the input tensor into two parts and using one part to gate the other, allowing for fine-grained control over the information flow.

Usefulness and How It Works
The GLU activation function is useful for tasks where understanding context and maintaining long-range dependencies in sequences is crucial. It’s designed to control the flow of information within a neural network’s hidden layers, making it particularly suitable for sequence modeling tasks.
How it Works
The GLU activation function takes a tensor x as input and performs the following steps:
- Split the input tensor x into two parts, usually along the last dimension. One part will be used for gating, and the other part will be used for input transformation.
- Apply a gating mechanism to the first part. This gating mechanism often involves the sigmoid activation function to produce values between 0 and 1, which control the flow of information.
- Multiply the transformed second part of the input tensor with the gated values obtained from the first part. This operation effectively controls how much information is passed through based on the gate values.
Consider an example of a neural network used for language translation. In this task, the network takes a sequence of words in one language and generates a sequence of words in another language. Maintaining context and understanding long-range dependencies between words is essential.
When a sentence is translated, certain words may have a significant impact on the translation of others. The GLU activation function can help capture these dependencies by allowing the network to gate certain information based on the context. For instance, when translating “I love cats,” the network might use GLU to identify that the verb “love” is crucial for determining the subject “cats” and the overall meaning of the sentence.
The Gated Linear Unit (GLU) activation function is useful for sequence-to-sequence tasks where maintaining context and understanding long-range dependencies in sequences is important. By splitting the input and using a gating mechanism, GLU provides fine-grained control over information flow, allowing the network to capture intricate relationships within sequences. It’s particularly effective for tasks like language translation, text generation, and other sequence modeling tasks.
Sinc Function
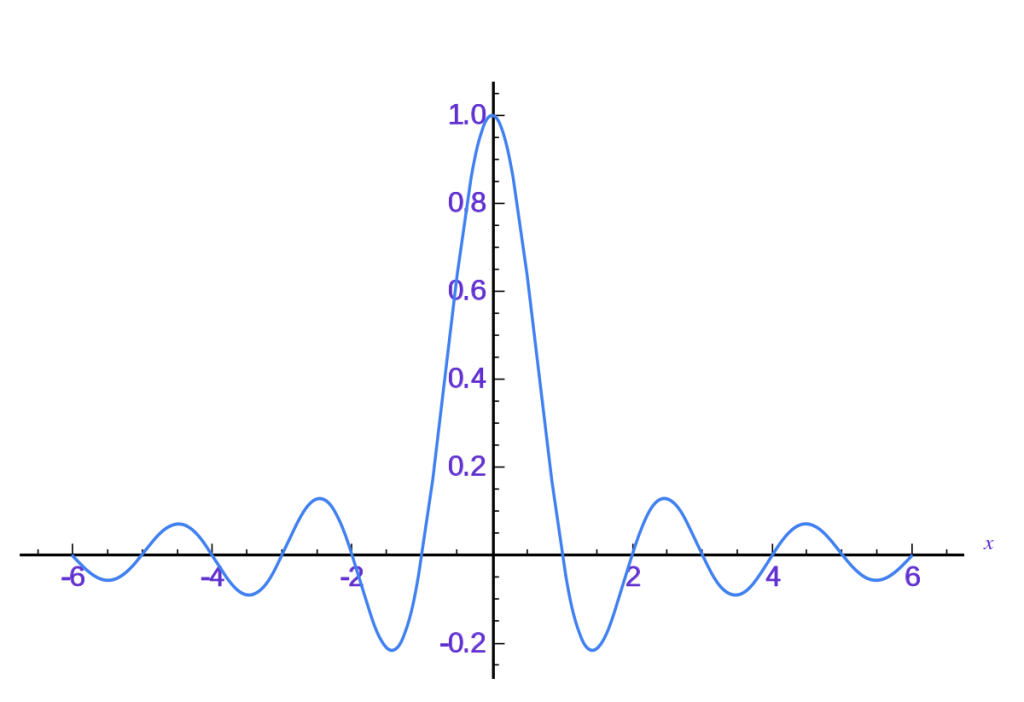
The Sinc function is a mathematical function defined as the sine of its argument divided by its argument.
Formula

Here, ‘x’ is the input value of the function.
How It’s Useful
Low-Pass Filtering: The Sinc function acts as a low-pass filter in the frequency domain. It is used to remove high-frequency components from signals while preserving low-frequency components. This property is valuable in image and signal processing tasks where you want to remove noise or high-frequency artifacts from data.
Aliasing Detection: The Sinc function’s zero crossings correspond to points of constructive or destructive interference. This property can be useful in applications involving aliasing detection and analysis, which is important in signal processing and image reconstruction tasks.
Let’s consider an example of using the Sinc function in a neural network architecture for image denoising. In this task, the network takes a noisy image as input and aims to produce a clean, denoised version of the image.
The Sinc function can be used as a part of a convolutional layer to perform a specific type of filtering. By convolving the input image with the Sinc function, the network can emphasize low-frequency components while suppressing high-frequency noise. This operation effectively removes high-frequency noise from the image while preserving the important structures and features.
The Sinc function is useful in certain applications, particularly in specific convolutional layers of neural networks where low-pass filtering and aliasing detection are required. Its unique properties make it suitable for tasks involving noise reduction, signal processing, and image reconstruction. While it’s not a commonly used activation function in standard neural network architectures, it has value in specialized scenarios where its characteristics are beneficial.
Conclusion
In summary, activation functions play a pivotal role in neural networks by addressing non-linearity, enabling data transformation, and accommodating variability. They navigate complex boundaries, alleviate engineering challenges, and handle diverse data. These functions counter vanishing gradients and enhance adaptability for problem-solving. The range of activation functions like sigmoid, tanh, ReLU, Leaky ReLU, PReLU, ELU, Swish, SELU, Mish, softmax, GLU, and even the Sinc function offers enhanced generalization and flexibility, making them indispensable tools for efficient neural network architecture.